giải hộ với

Câu 1 Để tính \( Q = \log_{\sigma}(b^2c^3) \), ta sẽ sử dụng các tính chất của logarit và các giá trị đã cho. Trước tiên, ta biết rằng: \[ \log_a b = 2 \] \[ \log_a c = 3 \] Ta cần tính \( Q = \log_{\sigma}(b^2c^3) \). Áp dụng tính chất logarit \( \log_{\sigma}(xy) = \log_{\sigma}x + \log_{\sigma}y \): \[ Q = \log_{\sigma}(b^2c^3) = \log_{\sigma}(b^2) + \log_{\sigma}(c^3) \] Tiếp theo, áp dụng tính chất \( \log_{\sigma}(x^n) = n \log_{\sigma}x \): \[ \log_{\sigma}(b^2) = 2 \log_{\sigma}b \] \[ \log_{\sigma}(c^3) = 3 \log_{\sigma}c \] Do đó: \[ Q = 2 \log_{\sigma}b + 3 \log_{\sigma}c \] Bây giờ, ta cần chuyển đổi \( \log_{\sigma}b \) và \( \log_{\sigma}c \) về cơ sở \( a \). Ta sử dụng công thức thay đổi cơ sở của logarit: \[ \log_{\sigma}b = \frac{\log_a b}{\log_a \sigma} \] \[ \log_{\sigma}c = \frac{\log_a c}{\log_a \sigma} \] Thay vào biểu thức của \( Q \): \[ Q = 2 \left( \frac{\log_a b}{\log_a \sigma} \right) + 3 \left( \frac{\log_a c}{\log_a \sigma} \right) \] Biết rằng \( \log_a b = 2 \) và \( \log_a c = 3 \): \[ Q = 2 \left( \frac{2}{\log_a \sigma} \right) + 3 \left( \frac{3}{\log_a \sigma} \right) \] \[ Q = \frac{4}{\log_a \sigma} + \frac{9}{\log_a \sigma} \] \[ Q = \frac{4 + 9}{\log_a \sigma} \] \[ Q = \frac{13}{\log_a \sigma} \] Vậy giá trị của \( Q \) là: \[ Q = \frac{13}{\log_a \sigma} \] Câu 2 Để tính \(2 \cdot a^{6b}\) khi biết \(a^{2b} = 5\), ta thực hiện các bước sau: Bước 1: Xác định giá trị của \(a^{6b}\). Ta có: \[ a^{6b} = (a^{2b})^3 \] Bước 2: Thay giá trị \(a^{2b} = 5\) vào biểu thức trên. \[ a^{6b} = 5^3 \] \[ a^{6b} = 125 \] Bước 3: Tính \(2 \cdot a^{6b}\). \[ 2 \cdot a^{6b} = 2 \cdot 125 \] \[ 2 \cdot a^{6b} = 250 \] Vậy, giá trị của \(2 \cdot a^{6b}\) là 250. Câu 3 Để tính xác suất cả hai xạ thủ đều không bắn trúng mục tiêu, ta thực hiện các bước sau: 1. Xác định xác suất của các biến cố: - Xác suất xạ thủ An bắn trúng mục tiêu là \( P(A) = 0,6 \). - Xác suất xạ thủ Bình bắn trúng mục tiêu là \( P(B) = 0,7 \). 2. Tìm xác suất của các biến cố đối: - Xác suất xạ thủ An không bắn trúng mục tiêu là \( P(\bar{A}) = 1 - P(A) = 1 - 0,6 = 0,4 \). - Xác suất xạ thủ Bình không bắn trúng mục tiêu là \( P(\bar{B}) = 1 - P(B) = 1 - 0,7 = 0,3 \). 3. Tính xác suất cả hai xạ thủ đều không bắn trúng mục tiêu: - Vì hai xạ thủ bắn vào cùng một mục tiêu ở hai thời điểm khác nhau, nên các biến cố này là độc lập. - Xác suất cả hai xạ thủ đều không bắn trúng mục tiêu là \( P(\bar{A} \cap \bar{B}) = P(\bar{A}) \times P(\bar{B}) = 0,4 \times 0,3 = 0,12 \). Vậy xác suất cả hai xạ thủ đều không bắn trúng mục tiêu là \( 0,12 \). 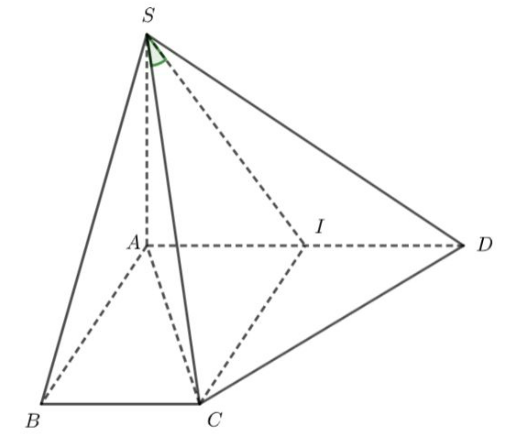Câu 4: a) Ta có \( AB \perp BC \) (vì \( ABCD \) là hình thang vuông tại \( A \) và \( B \)) và \( SA \perp (ABCD) \) (theo đề bài). Do đó, \( SA \perp BC \). Vì \( BC \) vuông góc với hai đường thẳng cắt nhau \( AB \) và \( SA \) trong mặt phẳng \( (SAB) \), nên \( BC \perp (SAB) \). Từ đó, ta suy ra \( BC \perp SB \). Vậy tam giác \( SBC \) vuông tại \( B \). b) Để xác định và tính góc giữa \( SC \) và mặt phẳng \( (SAD) \), ta thực hiện các bước sau: - Xác định giao điểm của \( SC \) với mặt phẳng \( (SAD) \): Gọi \( H \) là chân đường cao hạ từ \( C \) xuống \( AD \). Vì \( ABCD \) là hình thang vuông tại \( A \) và \( B \), ta có \( H \) nằm trên \( AD \) sao cho \( CH \perp AD \). - Xác định góc giữa \( SC \) và mặt phẳng \( (SAD) \): Góc giữa \( SC \) và mặt phẳng \( (SAD) \) là góc giữa \( SC \) và \( SH \), tức là góc \( \angle SCH \). - Tính góc \( \angle SCH \): Ta có: \[ CH = BC = a \] \[ SH = \sqrt{SC^2 - CH^2} \] Trước tiên, tính \( SC \): \[ SC = \sqrt{SB^2 + BC^2} = \sqrt{(a\sqrt{2})^2 + a^2} = \sqrt{2a^2 + a^2} = \sqrt{3a^2} = a\sqrt{3} \] Tiếp theo, tính \( SH \): \[ SH = \sqrt{(a\sqrt{3})^2 - a^2} = \sqrt{3a^2 - a^2} = \sqrt{2a^2} = a\sqrt{2} \] Vậy: \[ \sin(\angle SCH) = \frac{CH}{SC} = \frac{a}{a\sqrt{3}} = \frac{1}{\sqrt{3}} \] Do đó: \[ \angle SCH = \arcsin\left(\frac{1}{\sqrt{3}}\right) \] Kết luận: Góc giữa \( SC \) và mặt phẳng \( (SAD) \) là \( \arcsin\left(\frac{1}{\sqrt{3}}\right) \). Câu 5: Sau 1 tháng, số tiền lãi phải trả là: \[ 100 \times 0,7\% = 100 \times \frac{0,7}{100} = 0,7 \text{ (triệu đồng)} \] Sau 1 tháng, số tiền gốc còn lại chưa trả là: \[ 100 - 5 + 0,7 = 95,7 \text{ (triệu đồng)} \] Sau 2 tháng, số tiền lãi phải trả là: \[ 95,7 \times 0,7\% = 95,7 \times \frac{0,7}{100} = 0,6699 \text{ (triệu đồng)} \] Sau 2 tháng, số tiền gốc còn lại chưa trả là: \[ 95,7 - 5 + 0,6699 = 91,3699 \text{ (triệu đồng)} \] Ta thấy rằng mỗi tháng số tiền gốc còn lại giảm dần và số tiền lãi cũng giảm dần theo. Để tìm số tháng cần thiết để trả hết nợ, ta sẽ tính toán tiếp tục cho đến khi số tiền gốc còn lại nhỏ hơn hoặc bằng 5 triệu đồng (vì mỗi tháng trả 5 triệu đồng). Sau 3 tháng, số tiền lãi phải trả là: \[ 91,3699 \times 0,7\% = 91,3699 \times \frac{0,7}{100} = 0,6395893 \text{ (triệu đồng)} \] Sau 3 tháng, số tiền gốc còn lại chưa trả là: \[ 91,3699 - 5 + 0,6395893 = 87,0094893 \text{ (triệu đồng)} \] Sau 4 tháng, số tiền lãi phải trả là: \[ 87,0094893 \times 0,7\% = 87,0094893 \times \frac{0,7}{100} = 0,6090664251 \text{ (triệu đồng)} \] Sau 4 tháng, số tiền gốc còn lại chưa trả là: \[ 87,0094893 - 5 + 0,6090664251 = 82,6185557351 \text{ (triệu đồng)} \] Sau 5 tháng, số tiền lãi phải trả là: \[ 82,6185557351 \times 0,7\% = 82,6185557351 \times \frac{0,7}{100} = 0,5783298901457 \text{ (triệu đồng)} \] Sau 5 tháng, số tiền gốc còn lại chưa trả là: \[ 82,6185557351 - 5 + 0,5783298901457 = 78,1968856252457 \text{ (triệu đồng)} \] Sau 6 tháng, số tiền lãi phải trả là: \[ 78,1968856252457 \times 0,7\% = 78,1968856252457 \times \frac{0,7}{100} = 0,54737819937672 \text{ (triệu đồng)} \] Sau 6 tháng, số tiền gốc còn lại chưa trả là: \[ 78,1968856252457 - 5 + 0,54737819937672 = 73,74426382462242 \text{ (triệu đồng)} \] Sau 7 tháng, số tiền lãi phải trả là: \[ 73,74426382462242 \times 0,7\% = 73,74426382462242 \times \frac{0,7}{100} = 0,5162098467723569 \text{ (triệu đồng)} \] Sau 7 tháng, số tiền gốc còn lại chưa trả là: \[ 73,74426382462242 - 5 + 0,5162098467723569 = 69,26047367139478 \text{ (triệu đồng)} \] Sau 8 tháng, số tiền lãi phải trả là: \[ 69,26047367139478 \times 0,7\% = 69,26047367139478 \times \frac{0,7}{100} = 0,48482331569976346 \text{ (triệu đồng)} \] Sau 8 tháng, số tiền gốc còn lại chưa trả là: \[ 69,26047367139478 - 5 + 0,48482331569976346 = 64,74529698709454 \text{ (triệu đồng)} \] Sau 9 tháng, số tiền lãi phải trả là: \[ 64,74529698709454 \times 0,7\% = 64,74529698709454 \times \frac{0,7}{100} = 0,4532170789096618 \text{ (triệu đồng)} \] Sau 9 tháng, số tiền gốc còn lại chưa trả là: \[ 64,74529698709454 - 5 + 0,4532170789096618 = 60,1985140660042 \text{ (triệu đồng)} \] Sau 10 tháng, số tiền lãi phải trả là: \[ 60,1985140660042 \times 0,7\% = 60,1985140660042 \times \frac{0,7}{100} = 0,4213895984620294 \text{ (triệu đồng)} \] Sau 10 tháng, số tiền gốc còn lại chưa trả là: \[ 60,1985140660042 - 5 + 0,4213895984620294 = 55,62090366446623 \text{ (triệu đồng)} \] Sau 11 tháng, số tiền lãi phải trả là: \[ 55,62090366446623 \times 0,7\% = 55,62090366446623 \times \frac{0,7}{100} = 0,3893463256512636 \text{ (triệu đồng)} \] Sau 11 tháng, số tiền gốc còn lại chưa trả là: \[ 55,62090366446623 - 5 + 0,3893463256512636 = 50,91024998911749 \text{ (triệu đồng)} \] Sau 12 tháng, số tiền lãi phải trả là: \[ 50,91024998911749 \times 0,7\% = 50,91024998911749 \times \frac{0,7}{100} = 0,3563717499238224 \text{ (triệu đồng)} \] Sau 12 tháng, số tiền gốc còn lại chưa trả là: \[ 50,91024998911749 - 5 + 0,3563717499238224 = 46,26662173904131 \text{ (triệu đồng)} \] Sau 13 tháng, số tiền lãi phải trả là: \[ 46,26662173904131 \times 0,7\% = 46,26662173904131 \times \frac{0,7}{100} = 0,3238663521732892 \text{ (triệu đồng)} \] Sau 13 tháng, số tiền gốc còn lại chưa trả là: \[ 46,26662173904131 - 5 + 0,3238663521732892 = 41,59048809121459 \text{ (triệu đồng)} \] Sau 14 tháng, số tiền lãi phải trả là: \[ 41,59048809121459 \times 0,7\% = 41,59048809121459 \times \frac{0,7}{100} = 0,2911334166385021 \text{ (triệu đồng)} \] Sau 14 tháng, số tiền gốc còn lại chưa trả là: \[ 41,59048809121459 - 5 + 0,291134166385021 = 36,88162225759961 \text{ (triệu đồng)} \] Sau 15 tháng, số tiền lãi phải trả là: \[ 36,88162225759961 \times 0,7\% = 36,88162225759961 \times \frac{0,7}{100} = 0,2581713558031973 \text{ (triệu đồng)} \] Sau 15 tháng, số tiền gốc còn lại chưa trả là: \[ 36,88162225759961 - 5 + 0,2581713558031973 = 32,13979361340281 \text{ (triệu đồng)} \] Sau 16 tháng, số tiền lãi phải trả là: \[ 32,13979361340281 \times 0,7\% = 32,13979361340281 \times \frac{0,7}{100} = 0,2249785552938197 \text{ (triệu đồng)} \] Sau 16 tháng, số tiền gốc còn lại chưa trả là: \[ 32,13979361340281 - 5 + 0,2249785552938197 = 27,36477216869663 \text{ (triệu đồng)} \] Sau 17 tháng, số tiền lãi phải trả là: \[ 27,36477216869663 \times 0,7\% = 27,36477216869663 \times \frac{0,7}{100} = 0,1915534051808764 \text{ (triệu đồng)} \] Sau 17 tháng, số tiền gốc còn lại chưa trả là: \[ 27,36477216869663 - 5 + 0,1915534051808764 = 22,55632557387751 \text{ (triệu đồng)} \] Sau 18 tháng, số tiền lãi phải trả là: \[ 22,55632557387751 \times 0,7\% = 22,55632557387751 \times \frac{0,7}{100} = 0,1578942790171426 \text{ (triệu đồng)} \] Sau 18 tháng, số tiền gốc còn lại chưa trả là: \[ 22,55632557387751 - 5 + 0,1578942790171426 = 17,71421985289465 \text{ (triệu đồng)} \] Sau 19 tháng, số tiền lãi phải trả là: \[ 17,71421985289465 \times 0,7\% = 17,71421985289465 \times \frac{0,7}{100} = 0,12400053897026255 \text{ (triệu đồng)} \] Sau 19 tháng, số tiền gốc còn lại chưa trả là: \[ 17,71421985289465 - 5 + 0,12400053897026255 = 12,83822039186491 \text{ (triệu đồng)} \] Sau 20 tháng, số tiền lãi phải trả là: \[ 12,83822039186491 \times 0,7\% = 12,83822039186491 \times \frac{0,7}{100} = 0,08986754274305437 \text{ (triệu đồng)} \] Sau 20 tháng, số tiền gốc còn lại chưa trả là: \[ 12,83822039186491 - 5 + 0,08986754274305437 = 7,928087934607964 \text{ (triệu đồng)} \] Sau 21 tháng, số tiền lãi phải trả là: \[ 7,928087934607964 \times 0,7\% = 7,928087934607964 \times \frac{0,7}{100} = 0,05549661554225575 \text{ (triệu đồng)} \] Sau 21 tháng, số tiền gốc còn lại chưa trả là: \[ 7,928087934607964 - 5 + 0,05549661554225575 = 2,983584549150219 \text{ (triệu đồng)} \] Sau 22 tháng, số tiền lãi phải trả là: \[ 2,983584549150219 \times 0,7\% = 2,983584549150219 \times \frac{0,7}{100} = 0,020885091844051534 \text{ (triệu đồng)} \] Sau 22 tháng, số tiền gốc còn lại chưa trả là: \[ 2,983584549150219 - 5 + 0,020885091844051534 = -1,995530359005739 \text{ (triệu đồng)} \] Như vậy, sau 22 tháng, số tiền gốc còn lại đã nhỏ hơn 0, tức là anh An đã trả hết nợ ngân hàng. Đáp số: Sau 22 tháng, anh An trả được hết nợ ngân hàng.