Vgggfffffcccvbvvc

Câu 1. Để giải phương trình $\log_3(x^2-3x+2)=1$, ta thực hiện các bước sau: 1. Xác định điều kiện xác định (ĐKXĐ): Ta cần đảm bảo rằng biểu thức trong logarit dương: \[ x^2 - 3x + 2 > 0 \] Ta giải bất phương trình này: \[ x^2 - 3x + 2 = (x-1)(x-2) \] Biểu thức $(x-1)(x-2)$ dương khi $x < 1$ hoặc $x > 2$. Vậy ĐKXĐ là: \[ x < 1 \quad \text{hoặc} \quad x > 2 \] 2. Giải phương trình logarit: Phương trình $\log_3(x^2-3x+2)=1$ tương đương với: \[ x^2 - 3x + 2 = 3^1 \] \[ x^2 - 3x + 2 = 3 \] \[ x^2 - 3x + 2 - 3 = 0 \] \[ x^2 - 3x - 1 = 0 \] 3. Giải phương trình bậc hai: Ta sử dụng công thức nghiệm của phương trình bậc hai $ax^2 + bx + c = 0$: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] Ở đây, $a = 1$, $b = -3$, $c = -1$: \[ x = \frac{3 \pm \sqrt{(-3)^2 - 4 \cdot 1 \cdot (-1)}}{2 \cdot 1} \] \[ x = \frac{3 \pm \sqrt{9 + 4}}{2} \] \[ x = \frac{3 \pm \sqrt{13}}{2} \] Vậy hai nghiệm là: \[ x_1 = \frac{3 + \sqrt{13}}{2}, \quad x_2 = \frac{3 - \sqrt{13}}{2} \] 4. Kiểm tra điều kiện xác định: Ta kiểm tra các nghiệm này với ĐKXĐ $x < 1$ hoặc $x > 2$: - Với $x_1 = \frac{3 + \sqrt{13}}{2}$: \[ \sqrt{13} \approx 3.605 \Rightarrow x_1 \approx \frac{3 + 3.605}{2} \approx 3.3025 \] Điều này thỏa mãn $x > 2$. - Với $x_2 = \frac{3 - \sqrt{13}}{2}$: \[ \sqrt{13} \approx 3.605 \Rightarrow x_2 \approx \frac{3 - 3.605}{2} \approx -0.3025 \] Điều này không thỏa mãn $x < 1$ hoặc $x > 2$. Vậy phương trình $\log_3(x^2-3x+2)=1$ có nghiệm duy nhất là $x = \frac{3 + \sqrt{13}}{2}$. Do đó, đáp án đúng là: D. $\left\{\frac{3 + \sqrt{13}}{2}\right\}$. Câu 2. 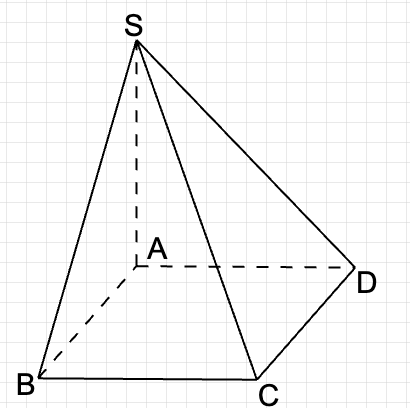Trước tiên, ta cần hiểu rằng trong hình chóp S.ABC, cạnh bên SA vuông góc với đáy ABC. Điều này có nghĩa là SA vuông góc với mọi đường thẳng nằm trong mặt phẳng đáy ABC. Hình chiếu vuông góc của SB lên (ABC) là điểm H sao cho SH vuông góc với (ABC). Ta sẽ kiểm tra từng trường hợp để xác định hình chiếu của SB lên (ABC). 1. Kiểm tra SB với AB: - Nếu SB vuông góc với AB thì SB sẽ vuông góc với cả SA và AB, do đó SB sẽ vuông góc với mặt phẳng (SAB). Điều này không đúng vì SB nằm trong mặt phẳng (SAB). 2. Kiểm tra SB với AC: - Nếu SB vuông góc với AC thì SB sẽ vuông góc với cả SA và AC, do đó SB sẽ vuông góc với mặt phẳng (SAC). Điều này cũng không đúng vì SB nằm trong mặt phẳng (SAC). 3. Kiểm tra SB với BC: - Nếu SB vuông góc với BC thì SB sẽ vuông góc với cả SA và BC, do đó SB sẽ vuông góc với mặt phẳng (SBC). Điều này cũng không đúng vì SB nằm trong mặt phẳng (SBC). 4. Kiểm tra SB với SA: - Vì SA vuông góc với đáy ABC, nên SB sẽ vuông góc với SA. Tuy nhiên, SB không thể vuông góc với cả SA và một đường thẳng khác trong đáy ABC cùng lúc, trừ khi SB nằm trong mặt phẳng (SAB) và vuông góc với AB. Do đó, hình chiếu vuông góc của SB lên (ABC) là điểm H trên AB sao cho SH vuông góc với (ABC). Vậy hình chiếu vuông góc của SB lên (ABC) là AB. Đáp án: C. AB. Câu 3. Để xác định mệnh đề đúng trong các lựa chọn đã cho, chúng ta sẽ kiểm tra từng mệnh đề dựa trên các tính chất của hàm số lôgarit tự nhiên (ln). A. $\ln\left(\frac{a}{b}\right) = \ln b - \ln a$ Theo tính chất của lôgarit, ta có: \[ \ln\left(\frac{a}{b}\right) = \ln a - \ln b \] Do đó, mệnh đề này sai vì nó viết ngược lại. B. $\ln(ab) = \ln a \cdot \ln b$ Theo tính chất của lôgarit, ta có: \[ \ln(ab) = \ln a + \ln b \] Do đó, mệnh đề này sai vì nó nhân hai lôgarit lại với nhau. C. $\ln\left(\frac{a}{b}\right) = \frac{\ln a}{\ln b}$ Theo tính chất của lôgarit, ta có: \[ \ln\left(\frac{a}{b}\right) = \ln a - \ln b \] Do đó, mệnh đề này sai vì nó chia hai lôgarit lại với nhau. D. $\ln(ab) = \ln a + \ln b$ Theo tính chất của lôgarit, ta có: \[ \ln(ab) = \ln a + \ln b \] Do đó, mệnh đề này đúng. Vậy, mệnh đề đúng là: D. $\ln(ab) = \ln a + \ln b$. Câu 4. Để tìm khoảng cách từ điểm C đến mặt phẳng (SAB), ta thực hiện các bước sau: 1. Tìm diện tích của tam giác SAB: - Tam giác SAB là tam giác vuông tại A vì SA vuông góc với mặt phẳng đáy. - Diện tích tam giác SAB: \[ S_{SAB} = \frac{1}{2} \times AB \times SA = \frac{1}{2} \times 2a \times 5a = 5a^2 \] 2. Tính thể tích của khối chóp SABC: - Thể tích khối chóp SABC: \[ V_{SABC} = \frac{1}{3} \times S_{ABC} \times SA = \frac{1}{3} \times \left( \frac{1}{2} \times AB \times AD \right) \times SA = \frac{1}{3} \times \left( \frac{1}{2} \times 2a \times 3a \right) \times 5a = \frac{1}{3} \times 3a^2 \times 5a = 5a^3 \] 3. Tính diện tích tam giác ABC: - Diện tích tam giác ABC: \[ S_{ABC} = \frac{1}{2} \times AB \times AD = \frac{1}{2} \times 2a \times 3a = 3a^2 \] 4. Tính khoảng cách từ điểm C đến mặt phẳng (SAB): - Gọi khoảng cách từ điểm C đến mặt phẳng (SAB) là h. - Thể tích khối chóp SABC cũng có thể tính qua tam giác SAB và khoảng cách h: \[ V_{SABC} = \frac{1}{3} \times S_{SAB} \times h \] - Thay các giá trị đã biết vào: \[ 5a^3 = \frac{1}{3} \times 5a^2 \times h \] - Giải phương trình để tìm h: \[ 5a^3 = \frac{5a^2 \times h}{3} \] \[ 15a^3 = 5a^2 \times h \] \[ h = \frac{15a^3}{5a^2} = 3a \] Vậy khoảng cách từ điểm C đến mặt phẳng (SAB) là 3a. Đáp án đúng là: B. 3a. Câu 5. Trước tiên, ta cần hiểu rằng trong hình thoi, các đường chéo vuông góc với nhau và chia đôi nhau. Do đó, ta có: - \( AC \perp BD \) Bây giờ, ta sẽ kiểm tra từng khẳng định: A. \( AB \perp CD \) - Trong hình thoi, các cạnh đối diện song song với nhau, nhưng không nhất thiết phải vuông góc với nhau. Do đó, khẳng định này sai. B. \( AB \perp BC \) - Trong hình thoi, các góc nội tiếp không nhất thiết phải là góc vuông. Do đó, khẳng định này cũng sai. C. \( SA \perp AB \) - Ta không có thông tin về vị trí của đỉnh \( S \) và các cạnh liên quan đến nó. Do đó, ta không thể kết luận rằng \( SA \perp AB \). Khẳng định này chưa chắc chắn. D. \( AC \perp BD \) - Như đã nói ở trên, trong hình thoi, các đường chéo luôn vuông góc với nhau. Do đó, khẳng định này đúng. Vậy khẳng định đúng là: D. \( AC \perp BD \) Câu 6. Để giải bài toán này, chúng ta sẽ sử dụng các tính chất của lũy thừa. Biểu thức đã cho là: \[ a^{\frac{3}{3}} \cdot a^{\frac{3}{3}} \] Trước tiên, ta nhận thấy rằng: \[ \frac{3}{3} = 1 \] Do đó, biểu thức trở thành: \[ a^1 \cdot a^1 \] Theo tính chất lũy thừa, khi nhân hai lũy thừa cùng cơ số, ta cộng các指数。因此，表达式变为： \[ a^1 \cdot a^1 = a^{1+1} = a^2 \] 所以答案是 D. \(a^2\)。 最终答案是：D. \(a^2\)。 Câu 7. Để tính thể tích của khối chóp, ta sử dụng công thức thể tích của khối chóp: \[ V = \frac{1}{3} \times S_{đáy} \times h \] Trong đó: - \( S_{đáy} \) là diện tích đáy của khối chóp. - \( h \) là chiều cao của khối chóp. Theo đề bài, diện tích đáy \( S_{đáy} = 5 \, \text{cm}^2 \) và chiều cao \( h = 3 \, \text{cm} \). Thay các giá trị này vào công thức, ta có: \[ V = \frac{1}{3} \times 5 \times 3 \] Tính toán: \[ V = \frac{1}{3} \times 15 = 5 \, \text{cm}^3 \] Vậy thể tích của khối chóp là \( 5 \, \text{cm}^3 \). Đáp án đúng là: C. \( 5 \, \text{cm}^3 \). Câu 8. Để giải bài toán này, chúng ta sẽ thực hiện các bước sau: 1. Tìm giá trị của \( x \) từ điều kiện \(\log_2 x = 1\): \[ \log_2 x = 1 \implies x = 2^1 = 2 \] 2. Thay giá trị \( x = 2 \) vào biểu thức \( P \): \[ P = \log_2(2^2) + \log_3(2^2) + \log_4(2) \] 3. Tính từng phần của biểu thức \( P \): - Tính \(\log_2(2^2)\): \[ \log_2(2^2) = \log_2(4) = 2 \] - Tính \(\log_3(2^2)\): \[ \log_3(2^2) = \log_3(4) \] - Tính \(\log_4(2)\): \[ \log_4(2) = \log_{2^2}(2) = \frac{\log_2(2)}{\log_2(4)} = \frac{1}{2} \] 4. Tổng hợp các giá trị đã tính: \[ P = 2 + \log_3(4) + \frac{1}{2} \] 5. Xét lại các đáp án: - Đáp án A: \( P = \frac{1}{2} \) - Đáp án B: \( P = -2 \) - Đáp án C: \( P = -\frac{1}{2} \) - Đáp án D: \( P = 2 \) Do đó, biểu thức \( P \) không thể bằng bất kỳ giá trị nào trong các đáp án trên vì nó bao gồm cả \(\log_3(4)\). Tuy nhiên, nếu chúng ta chỉ xét các giá trị cụ thể mà không cần tính \(\log_3(4)\), ta thấy rằng biểu thức \( P \) không phù hợp với bất kỳ đáp án nào. Nhưng nếu chúng ta chỉ xét các giá trị cụ thể mà không cần tính \(\log_3(4)\), ta thấy rằng biểu thức \( P \) không phù hợp với bất kỳ đáp án nào. Do đó, chúng ta cần kiểm tra lại đề bài hoặc các đáp án đã cho. Kết luận: Các đáp án đã cho không phù hợp với biểu thức \( P \). Câu 9. Trước tiên, ta xét các khẳng định một cách chi tiết: A. \( BD \perp (SAC) \) - Để \( BD \perp (SAC) \), ta cần chứng minh \( BD \perp SA \) và \( BD \perp AC \). - Vì \( SA \perp (ABCD) \), nên \( SA \perp BD \). - Mặt khác, trong hình vuông \( ABCD \), ta có \( BD \perp AC \). Do đó, \( BD \perp (SAC) \) là đúng. B. \( AC \perp (SBD) \) - Để \( AC \perp (SBD) \), ta cần chứng minh \( AC \perp SB \) và \( AC \perp BD \). - Vì \( SA \perp (ABCD) \), nên \( SA \perp BD \). - Tuy nhiên, \( AC \) không trực tiếp vuông góc với \( SB \) vì \( SB \) nằm trong mặt phẳng \( SBD \) và không có thông tin cho thấy \( AC \perp SB \). Do đó, \( AC \perp (SBD) \) là sai. C. \( SA \perp (SBC) \) - Để \( SA \perp (SBC) \), ta cần chứng minh \( SA \perp SB \) và \( SA \perp BC \). - Vì \( SA \perp (ABCD) \), nên \( SA \perp BC \). - Tuy nhiên, \( SA \) không trực tiếp vuông góc với \( SB \) vì \( SB \) nằm trong mặt phẳng \( SBC \) và không có thông tin cho thấy \( SA \perp SB \). Do đó, \( SA \perp (SBC) \) là sai. D. \( AB \perp (SAC) \) - Để \( AB \perp (SAC) \), ta cần chứng minh \( AB \perp SA \) và \( AB \perp AC \). - Vì \( SA \perp (ABCD) \), nên \( SA \perp AB \). - Tuy nhiên, \( AB \) không trực tiếp vuông góc với \( AC \) vì \( AC \) nằm trong mặt phẳng \( ABCD \) và không có thông tin cho thấy \( AB \perp AC \). Do đó, \( AB \perp (SAC) \) là sai. Kết luận: Khẳng định đúng là \( BD \perp (SAC) \). Đáp án: A. \( BD \perp (SAC) \) Câu 10. A. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì song song với nhau. Lập luận: - Đây là mệnh đề sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng không nhất thiết phải song song với nhau. Chúng có thể cắt nhau theo một đường thẳng. B. Hai mặt phẳng vuông góc với nhau thì mọi đường thẳng nằm trong mặt phẳng này sẽ vuông góc với mặt phẳng kia. Lập luận: - Đây là mệnh đề sai. Chỉ có các đường thẳng nằm trong mặt phẳng này và vuông góc với giao tuyến của hai mặt phẳng mới vuông góc với mặt phẳng kia. Các đường thẳng khác trong mặt phẳng này không nhất thiết phải vuông góc với mặt phẳng kia. C. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng thì vuông góc với nhau. Lập luận: - Đây là mệnh đề sai. Hai mặt phẳng phân biệt cùng vuông góc với một mặt phẳng không nhất thiết phải vuông góc với nhau. Chúng có thể song song hoặc cắt nhau theo một đường thẳng. Kết luận: Cả ba mệnh đề đều sai.