giuppppppp

Câu 8. Để giải quyết câu hỏi này, chúng ta cần hiểu rõ về hình chiếu của đường thẳng lên mặt phẳng và đặc biệt là trong trường hợp đường thẳng vuông góc với mặt phẳng. 1. Hình chiếu của đường thẳng lên mặt phẳng: - Nếu đường thẳng \(a\) vuông góc với mặt phẳng \((P)\), thì hình chiếu của đường thẳng \(a\) lên mặt phẳng \((P)\) sẽ là điểm giao giữa đường thẳng \(a\) và mặt phẳng \((P)\). 2. Lý do: - Khi đường thẳng \(a\) vuông góc với mặt phẳng \((P)\), nó cắt mặt phẳng \((P)\) tại một điểm duy nhất. Điểm này chính là hình chiếu của đường thẳng \(a\) lên mặt phẳng \((P)\). Do đó, hình chiếu của đường thẳng \(a\) trên mặt phẳng \((P)\) là giao điểm \(H\) của đường thẳng \(a\) với mặt phẳng \((P)\). Đáp án đúng là: B. Là giao điểm \(H\) của đường thẳng \(a\) với mặt phẳng \((P)\). Câu 9. Để xác định góc giữa đường thẳng SC và mặt phẳng (ABC), ta thực hiện các bước sau: 1. Xác định trực giao: Vì \( SA \perp (ABC) \), nên đoạn thẳng SA là đường thẳng vuông góc hạ từ đỉnh S xuống mặt phẳng (ABC). 2. Xác định hình chiếu: Điểm A là hình chiếu của điểm S trên mặt phẳng (ABC). 3. Xác định góc giữa đường thẳng và mặt phẳng: Góc giữa đường thẳng SC và mặt phẳng (ABC) là góc giữa đường thẳng SC và hình chiếu của nó trên mặt phẳng (ABC). Hình chiếu của SC trên mặt phẳng (ABC) là đoạn thẳng AC. Do đó, góc giữa đường thẳng SC và mặt phẳng (ABC) là góc \( \angle SCA \). Vậy đáp án đúng là: C. SAC. Câu 10. Để giải phương trình $10^{1.5x} = 1000000$, ta thực hiện các bước sau: Bước 1: Viết lại phương trình dưới dạng cơ số giống nhau: \[ 10^{1.5x} = 10^6 \] Bước 2: So sánh các mũ của cơ số 10: \[ 1.5x = 6 \] Bước 3: Giải phương trình để tìm giá trị của \( x \): \[ x = \frac{6}{1.5} \] \[ x = 4 \] Vậy nghiệm của phương trình là \( x = 4 \). Do đó, đáp án đúng là: D. \( x = 4 \). Câu 11. Để kiểm tra tính đúng đắn của các mệnh đề, chúng ta sẽ áp dụng các công thức và tính chất của logarit. A. $\log_x(\frac{x}{y}) = \log_x x - \log_x y$ Theo tính chất của logarit: \[ \log_x(\frac{x}{y}) = \log_x x - \log_x y \] Đúng vì theo tính chất chia của logarit: $\log_b(\frac{m}{n}) = \log_b m - \log_b n$. B. $\log_x(\frac{1}{x}) = \frac{1}{\log_x x}$ Theo tính chất của logarit: \[ \log_x(\frac{1}{x}) = \log_x(1) - \log_x(x) = 0 - 1 = -1 \] Mặt khác, $\log_x x = 1$, do đó $\frac{1}{\log_x x} = \frac{1}{1} = 1$. Như vậy, $\log_x(\frac{1}{x}) = -1$ và $\frac{1}{\log_x x} = 1$, nên mệnh đề này sai. C. $\log_s a \cdot \log_s x = \log_s x$ Đây là một mệnh đề không đúng vì không có tính chất nào của logarit cho phép nhân hai logarit như vậy và kết quả là một logarit khác. D. $\log_x(xy) = \log_x x + \log_x y$ Theo tính chất của logarit: \[ \log_x(xy) = \log_x x + \log_x y \] Đúng vì theo tính chất nhân của logarit: $\log_b(mn) = \log_b m + \log_b n$. Tóm lại, mệnh đề sai là: B. $\log_x(\frac{1}{x}) = \frac{1}{\log_x x}$ Câu 12. Để giải bài toán này, chúng ta sẽ sử dụng các tính chất của logarit để biến đổi biểu thức $\log_x(a^2b)$. Bước 1: Áp dụng tính chất logarit $\log_x(ab) = \log_x(a) + \log_x(b)$: \[ \log_x(a^2b) = \log_x(a^2) + \log_x(b) \] Bước 2: Áp dụng tính chất logarit $\log_x(a^n) = n \cdot \log_x(a)$: \[ \log_x(a^2) = 2 \cdot \log_x(a) \] Bước 3: Thay vào biểu thức ban đầu: \[ \log_x(a^2b) = 2 \cdot \log_x(a) + \log_x(b) \] Như vậy, biểu thức $\log_x(a^2b)$ bằng $2 \cdot \log_x(a) + \log_x(b)$. Do đó, đáp án đúng là: D. $2 + \log_x(b)$ Đáp số: D. $2 + \log_x(b)$. Câu 1. Điều kiện: \( x > 1 \) Phương trình đã cho: \[ \log_3(x + 6) = \log_3(x - 1) + 1 \] Ta có thể viết lại phương trình này dưới dạng: \[ \log_3(x + 6) = \log_3(x - 1) + \log_3(3) \] \[ \log_3(x + 6) = \log_3(3(x - 1)) \] Do đó: \[ x + 6 = 3(x - 1) \] \[ x + 6 = 3x - 3 \] \[ 6 + 3 = 3x - x \] \[ 9 = 2x \] \[ x = \frac{9}{2} \] Kiểm tra điều kiện: \[ x = \frac{9}{2} > 1 \] Vậy nghiệm của phương trình là \( x = \frac{9}{2} \). Đáp án đúng là: \[ x = \frac{9}{2} \] Đáp án: \( x = \frac{9}{2} \) Câu 2. 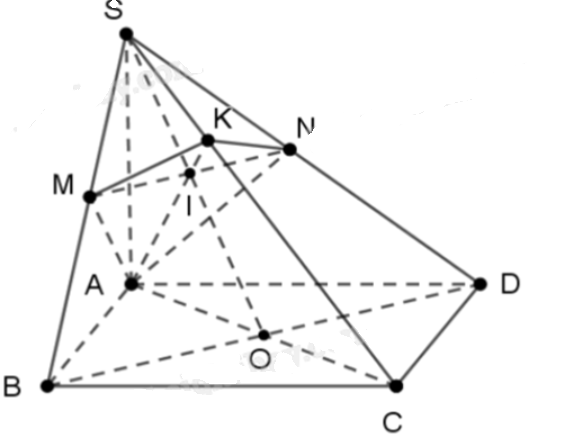a) Đúng vì SA vuông góc với đáy ABCD nên SA vuông góc với mọi đường thẳng nằm trong đáy, bao gồm cả AO. b) Sai vì AM vuông góc với SB (do M là hình chiếu của A trên SB) và AM vuông góc với SD (do N là hình chiếu của A trên SD). Vì vậy, AM vuông góc với mặt phẳng SBD, do đó AM cũng vuông góc với mọi đường thẳng nằm trong mặt phẳng SBD, bao gồm cả SC. Do đó, AM vuông góc với mặt phẳng SBC. c) Đúng vì K là giao điểm của SC với mặt phẳng (AMN), do đó K thuộc SC và mặt phẳng (AMN). Vì AM và AN đều vuông góc với SD và SB, nên AM và AN cũng vuông góc với mọi đường thẳng nằm trong mặt phẳng SBD, bao gồm cả SK. Do đó, AMKN là tứ giác có hai cặp cạnh vuông góc với nhau. d) Đúng vì AC nằm trong mặt phẳng ABCD và SBD là mặt phẳng đi qua đỉnh S và cắt đáy ABCD theo đường chéo BD. Vì SA vuông góc với đáy ABCD, nên SBD cũng vuông góc với đáy ABCD. Do đó, AC vuông góc với SBD. Câu 1. Đầu tiên, ta tính năng lượng giải tỏa của trận động đất tại thành phố X vào năm 1995. Theo công thức đã cho, ta có: \[ \log(E_X) = 11,4 + 1,5 \times 8 \] \[ \log(E_X) = 11,4 + 12 = 23,4 \] Do đó: \[ E_X = 10^{23,4} \] Trận động đất tại thành phố Y vào năm 1997 có năng lượng giải tỏa là: \[ E_Y = \frac{E_X}{14} = \frac{10^{23,4}}{14} \] Ta cần tìm độ lớn M_Y của trận động đất tại thành phố Y. Theo công thức đã cho: \[ \log(E_Y) = 11,4 + 1,5 \times M_Y \] Thay \( E_Y = \frac{10^{23,4}}{14} \) vào, ta có: \[ \log\left(\frac{10^{23,4}}{14}\right) = 11,4 + 1,5 \times M_Y \] \[ \log(10^{23,4}) - \log(14) = 11,4 + 1,5 \times M_Y \] \[ 23,4 - \log(14) = 11,4 + 1,5 \times M_Y \] \[ 23,4 - 1,146 = 11,4 + 1,5 \times M_Y \] \[ 22,254 = 11,4 + 1,5 \times M_Y \] \[ 1,5 \times M_Y = 22,254 - 11,4 \] \[ 1,5 \times M_Y = 10,854 \] \[ M_Y = \frac{10,854}{1,5} \] \[ M_Y = 7,236 \] Vậy độ lớn của trận động đất tại thành phố Y là khoảng 7,24 độ Richte. Câu 2. Trước tiên, ta xác định góc giữa hai mặt phẳng (AHK) và (SBD). Gọi giao điểm của AC và BD là O. Vì ABCD là hình thoi nên O là trung điểm của cả AC và BD. Mặt khác, vì SA vuông góc với đáy ABCD, nên SA vuông góc với BD. Do đó, BD vuông góc với mặt phẳng SAC, suy ra BD vuông góc với SC. Vậy góc giữa hai mặt phẳng (AHK) và (SBD) chính là góc giữa đường thẳng AK và mặt phẳng SBD, tức là góc giữa AK và SO. Ta sẽ tính tan của góc này. Ta có: - Tam giác SAD là tam giác đều cạnh a, do đó SD = a. - Tam giác SAB cũng là tam giác đều cạnh a, do đó SB = a. - Tam giác SBD là tam giác cân tại S, do đó SO vuông góc với BD tại O. Ta tính SO: \[ SO = \sqrt{SB^2 - OB^2} = \sqrt{a^2 - \left(\frac{a\sqrt{3}}{2}\right)^2} = \sqrt{a^2 - \frac{3a^2}{4}} = \sqrt{\frac{a^2}{4}} = \frac{a}{2} \] Bây giờ, ta tính AK. Vì AK vuông góc với SN, nên AK là đường cao của tam giác ASN từ đỉnh A xuống cạnh SN. Ta có: \[ AN = \frac{AD}{2} = \frac{a}{2} \] \[ SN = \sqrt{SA^2 + AN^2} = \sqrt{a^2 + \left(\frac{a}{2}\right)^2} = \sqrt{a^2 + \frac{a^2}{4}} = \sqrt{\frac{5a^2}{4}} = \frac{a\sqrt{5}}{2} \] Diện tích tam giác ASN: \[ [ASN] = \frac{1}{2} \times SA \times AN = \frac{1}{2} \times a \times \frac{a}{2} = \frac{a^2}{4} \] Diện tích tam giác ASN cũng có thể tính qua đường cao AK: \[ [ASN] = \frac{1}{2} \times SN \times AK = \frac{1}{2} \times \frac{a\sqrt{5}}{2} \times AK = \frac{a\sqrt{5}}{4} \times AK \] Bằng nhau hai diện tích này: \[ \frac{a^2}{4} = \frac{a\sqrt{5}}{4} \times AK \] \[ AK = \frac{a}{\sqrt{5}} = \frac{a\sqrt{5}}{5} \] Cuối cùng, ta tính tan của góc giữa AK và SO: \[ \tan(\theta) = \frac{AK}{SO} = \frac{\frac{a\sqrt{5}}{5}}{\frac{a}{2}} = \frac{2\sqrt{5}}{5} \] Vậy, giá trị của tan góc giữa hai mặt phẳng (AHK) và (SBD) là $\frac{2\sqrt{5}}{5}$. Câu 3. Để giải bài toán này, chúng ta sẽ sử dụng các tính chất của logarit để biến đổi và tìm giá trị của biểu thức $\log_s b$. Bước 1: Biến đổi phương trình đã cho: \[ \log_{a^3} \frac{a^5}{\sqrt[4]{b}} = 2 \] Bước 2: Áp dụng công thức logarit cơ bản: \[ \log_{a^3} \left( a^5 \cdot b^{-\frac{1}{4}} \right) = 2 \] Bước 3: Sử dụng tính chất $\log_b(xy) = \log_b x + \log_b y$: \[ \log_{a^3} a^5 + \log_{a^3} b^{-\frac{1}{4}} = 2 \] Bước 4: Áp dụng tính chất $\log_b(x^n) = n \log_b x$: \[ 5 \log_{a^3} a - \frac{1}{4} \log_{a^3} b = 2 \] Bước 5: Biến đổi $\log_{a^3} a$: \[ \log_{a^3} a = \frac{\log_a a}{\log_a a^3} = \frac{1}{3} \] Do đó: \[ 5 \cdot \frac{1}{3} - \frac{1}{4} \log_{a^3} b = 2 \] Bước 6: Giải phương trình: \[ \frac{5}{3} - \frac{1}{4} \log_{a^3} b = 2 \] \[ - \frac{1}{4} \log_{a^3} b = 2 - \frac{5}{3} \] \[ - \frac{1}{4} \log_{a^3} b = \frac{6}{3} - \frac{5}{3} \] \[ - \frac{1}{4} \log_{a^3} b = \frac{1}{3} \] \[ \log_{a^3} b = -\frac{4}{3} \] Bước 7: Biến đổi $\log_{a^3} b$ thành $\log_a b$: \[ \log_{a^3} b = \frac{\log_a b}{\log_a a^3} = \frac{\log_a b}{3} \] Do đó: \[ \frac{\log_a b}{3} = -\frac{4}{3} \] \[ \log_a b = -4 \] Bước 8: Tìm giá trị của biểu thức $\log_s b$: \[ s = a \] \[ \log_s b = \log_a b = -4 \] Vậy giá trị của biểu thức $\log_s b$ là: \[ \boxed{-4} \] Câu 4. Để tính khoảng cách giữa hai đường thẳng AC và SB trong hình chóp S.ABCD, ta thực hiện các bước sau: 1. Xác định các điểm và vectơ: - Gọi O là tâm của hình vuông ABCD. - Ta có \( SA \perp (ABCD) \) và \( SA = 3a \). - Vì ABCD là hình vuông cạnh bằng \( a \), nên \( AC = a\sqrt{2} \). 2. Tìm vectơ pháp tuyến của mặt phẳng (SAC): - Mặt phẳng (SAC) chứa các điểm S, A và C. - Vectơ \( \overrightarrow{SA} = (0, 0, -3a) \). - Vectơ \( \overrightarrow{AC} = (a, a, 0) \). - Vectơ pháp tuyến \( \overrightarrow{n} \) của mặt phẳng (SAC) là tích vector của \( \overrightarrow{SA} \) và \( \overrightarrow{AC} \): \[ \overrightarrow{n} = \overrightarrow{SA} \times \overrightarrow{AC} = \begin{vmatrix} \mathbf{i} & \mathbf{j} & \mathbf{k} \\ 0 & 0 & -3a \\ a & a & 0 \end{vmatrix} = (3a^2, -3a^2, 0) \] 3. Tìm khoảng cách từ điểm B đến mặt phẳng (SAC): - Phương trình mặt phẳng (SAC) có dạng \( Ax + By + Cz + D = 0 \), với \( \overrightarrow{n} = (3a^2, -3a^2, 0) \). - Thay tọa độ của điểm S vào phương trình mặt phẳng để tìm \( D \): \[ 3a^2 \cdot 0 - 3a^2 \cdot 0 + 0 \cdot 3a + D = 0 \implies D = 0 \] - Vậy phương trình mặt phẳng (SAC) là: \[ 3a^2x - 3a^2y = 0 \implies x - y = 0 \] - Khoảng cách từ điểm B đến mặt phẳng (SAC) là: \[ d = \frac{|x_B - y_B|}{\sqrt{A^2 + B^2}} = \frac{|a - 0|}{\sqrt{(3a^2)^2 + (-3a^2)^2}} = \frac{a}{\sqrt{9a^4 + 9a^4}} = \frac{a}{3a^2\sqrt{2}} = \frac{1}{3a\sqrt{2}} \] 4. Kết luận: - Khoảng cách giữa hai đường thẳng AC và SB là: \[ d = \frac{a}{3\sqrt{2}} \] Đáp số: \( \frac{a}{3\sqrt{2}} \) Câu 5. Để giải quyết bài toán này, chúng ta cần xác định góc giữa mép BC của khối gỗ và lưỡi cắt của máy cắt khi cắt theo mặt phẳng (P) đi qua điểm C và song song với mặt phẳng (A'B'C'D'). 1. Xác định mặt phẳng (P): - Mặt phẳng (P) đi qua điểm C và song song với mặt phẳng (A'B'C'D'). - Vì (P) song song với (A'B'C'D'), nên (P) sẽ song song với các đường thẳng nằm trong (A'B'C'D'), bao gồm A'B', B'C', C'D', và D'A'. 2. Xác định góc giữa BC và lưỡi cắt: - Khi cắt theo mặt phẳng (P), lưỡi cắt sẽ tạo thành một đường thẳng trên mặt phẳng (P). - Vì (P) song song với (A'B'C'D'), nên lưỡi cắt sẽ song song với B'C'. - Góc giữa BC và lưỡi cắt chính là góc giữa BC và B'C'. 3. Xác định góc giữa BC và B'C': - Trên hình vẽ, B'C' là đường thẳng nằm trong mặt phẳng (A'B'C'D') và song song với B'C. - Góc giữa BC và B'C' chính là góc giữa hai đường thẳng này. 4. Tính góc: - Từ hình vẽ, ta thấy rằng B'C' là đường thẳng nằm trong mặt phẳng (A'B'C'D') và song song với B'C. - Góc giữa BC và B'C' là góc vuông (90 độ). Do đó, góc giữa mép BC của khối gỗ và lưỡi cắt của máy cắt là 90 độ. Đáp số: 90 độ. Câu 6. Giả sử số tiền ban đầu là 100% thì số tiền sau mỗi năm sẽ tăng thêm 8,4%. Số tiền sau 1 năm là: 100% + 8,4% = 108,4% = $\frac{108,4}{100}$ = 1,084 (so với ban đầu) Số tiền sau 2 năm là: 1,084 × 1,084 = 1,173936 (so với ban đầu) Số tiền sau 3 năm là: 1,084 × 1,084 × 1,084 = 1,271241024 (so với ban đầu) Số tiền sau 4 năm là: 1,084 × 1,084 × 1,084 × 1,084 = 1,378159157 (so với ban đầu) Số tiền sau 5 năm là: 1,084 × 1,084 × 1,084 × 1,084 × 1,084 = 1,497099184 (so với ban đầu) Số tiền sau 6 năm là: 1,084 × 1,084 × 1,084 × 1,084 × 1,084 × 1,084 = 1,631003586 (so với ban đầu) Số tiền sau 7 năm là: 1,084 × 1,084 × 1,084 × 1,084 × 1,084 × 1,084 × 1,084 = 1,783007998 (so với ban đầu) Số tiền sau 8 năm là: 1,084 × 1,084 × 1,084 × 1,084 × 1,084 × 1,084 × 1,084 × 1,084 = 1,956979797 (so với ban đầu) Như vậy, sau 8 năm, số tiền sẽ gấp hơn 1,95 lần so với ban đầu, gần gấp đôi. Vậy, sau ít nhất 8 năm, người đó sẽ thu được số tiền gấp đôi số tiền ban đầu.