06/04/2025
Giúp em với ạ

 0
0
Làm sao để có câu trả lời hay nhất?
- Luôn có GIẢI THÍCH các bước giải
- Không copy câu trả lời của Timi
- Không sao chép trên mạng
- Không spam câu trả lời để nhận điểm
- Spam sẽ bị khóa tài khoản



06/04/2025
 0
0
06/04/2025
Câu 5:
Đặt
Suy ra
Rõ ràng,
Áp dụng định lí Pythagore ta tính được:
Tổng khoảng cách từ hai vị trí
Xét hàm số
Ta có
Trên khoảng
Bảng biến thiên của hàm số
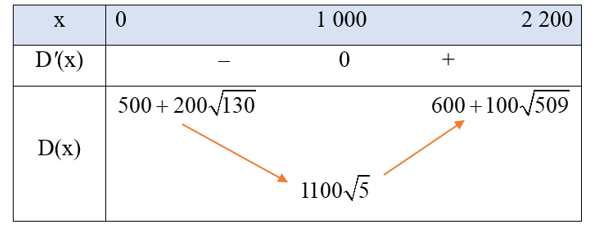
Căn cứ vào bảng biến thiên, ta thấy hàm số
 0
0
06/04/2025
Apple_6u2gxTkDHXTiykQJ9MM1b0oMZ213Chắc chắn rồi, dưới đây là lời giải chi tiết cho các bài toán bạn cung cấp:
Câu 2:
Phân tích: Người đưa thư phải đi qua tất cả các con đường màu đỏ ít nhất một lần và quay lại điểm xuất phát. Để tổng quãng đường ngắn nhất, người đưa thư nên đi theo chu trình Euler (nếu đồ thị có chu trình Euler) hoặc đường đi gần với chu trình Euler nhất.
Giải: Nhận thấy đồ thị có 6 đỉnh và 7 cạnh. Để đi qua tất cả các cạnh, người đưa thư cần đi qua mỗi cạnh một lần (nếu có thể) và quay lại điểm xuất phát. Tuy nhiên, đồ thị này không có chu trình Euler vì có 4 đỉnh bậc lẻ. Do đó, người đưa thư cần đi qua một số cạnh hai lần. Các cạnh cần đi hai lần là các cạnh nối 4 đỉnh bậc lẻ này. Để quãng đường ngắn nhất, ta cần chọn các cạnh đi hai lần sao cho tổng độ dài của chúng là nhỏ nhất.
Chọn các cạnh đi hai lần: 2 cạnh dọc phía trên và 2 cạnh dọc phía dưới.
Tổng độ dài các cạnh: 10 + 10 + 15 + 15 + 20 + 20 + 25 = 115
Tổng độ dài các cạnh đi hai lần: 10 + 10 + 15 + 15 = 50
Tổng quãng đường ngắn nhất: 115 + 50 = 165
Đáp số: 165
Câu 3:
Phân tích: Máy bay bay theo đường thẳng từ A đến B và hạ cánh tại M. Ta cần tìm tọa độ điểm M sao cho M nằm trên đoạn AB và M có cao độ z = 0.
Giải:
Vectơ AB = (10 - 15, 10 - 0, 3 - 5) = (-5, 10, -2)
Phương trình tham số của đường thẳng AB:x = 15 - 5t
y = 10t
z = 5 - 2t
Vì M(a, b, 0) nằm trên đoạn AB nên z = 0, suy ra 5 - 2t = 0 => t = 5/2
Thay t = 5/2 vào phương trình tham số, ta được:a = 15 - 5(5/2) = 5/2
b = 10(5/2) = 25
Vậy a + b = 5/2 + 25 = 55/2 = 27.5
Đáp số: 27.5
Câu 4:
Phân tích: Tính diện tích phần hình tròn chứa nhiên liệu, sau đó nhân với chiều dài bể để được thể tích.
Giải:
Diện tích phần hình tròn chứa nhiên liệu:Diện tích hình quạt tròn: S_quạt = (α/360)πr²
Diện tích tam giác tạo bởi hai bán kính và dây cung: S_tam giác = (1/2)r²sinα
Diện tích phần hình tròn chứa nhiên liệu: S = S_quạt - S_tam giác
Tính góc α:Sử dụng định lý cosin trong tam giác tạo bởi hai bán kính và dây cung.
Dây cung có độ dài: 2√(1² - (1 - 1.5)²) = √3
cosα = (1² + 1² - (√3)²) / (2 * 1 * 1) = -1/2 => α = 120°
Tính diện tích phần hình tròn chứa nhiên liệu:S_quạt = (120/360)π(1²) = π/3
S_tam giác = (1/2)(1²)sin120° = √3/4
S = π/3 - √3/4 ≈ 0.614
Tính thể tích nhiên liệu: V = S * chiều dài = 0.614 * 5 ≈ 3.07
Đáp số: 3.1
Câu 5:
Phân tích: Tìm điểm M trên đoạn AB sao cho MA + MB nhỏ nhất. Bài toán này liên quan đến tính chất đường gấp khúc.
Giải:
Lấy điểm A' đối xứng với A qua bờ sông.
Khi đó, MA = MA', nên MA + MB = MA' + MB.
MA' + MB nhỏ nhất khi A', M, B thẳng hàng.
Sử dụng định lý Pitago và tính chất tam giác đồng dạng để tìm MA' và MB.
Tính MA' và MB:A'B = √(2200² + (600 + 500)²) = √5929000 ≈ 2435
MA' = (500/1100) * 2435 ≈ 1107
MB = (600/1100) * 2435 ≈ 1328
MA + MB = MA' + MB ≈ 1107 + 1328 = 2435
Đáp số: 2435
Câu 6:
Phân tích: Tìm độ dài đường gấp khúc ngắn nhất bao quanh kim tự tháp. Bài toán này liên quan đến việc trải phẳng các mặt của hình chóp.
Giải:
Trải phẳng các mặt của hình chóp, ta được một hình quạt tròn có bán kính 200m và cung tròn có độ dài bằng chu vi đáy kim tự tháp.
Tính chu vi đáy kim tự tháp: C = 4 * cạnh đáy = 4 * 200 = 800m
Tính độ dài cung tròn của hình quạt: L = (α/360) * 2π * 200
Tính góc α:Sử dụng định lý cosin trong tam giác ASB để tìm góc α.
cos15° = (200² + 200² - AB²) / (2 * 200 * 200)
AB = 2 * 200 * sin(15°/2) ≈ 104
α ≈ 165°
Tính độ dài cung tròn: L ≈ (165/360) * 2π * 200 ≈ 576
Tính độ dài dây đèn led: 576 + 40 = 616
Đáp số: 616
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
2 phút trước
4 phút trước
7 phút trước
20 phút trước
Top thành viên trả lời



 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




