Giúp mình với!

Bùi Tú MinhChắc chắn rồi, hãy cùng giải bài toán hình học này:

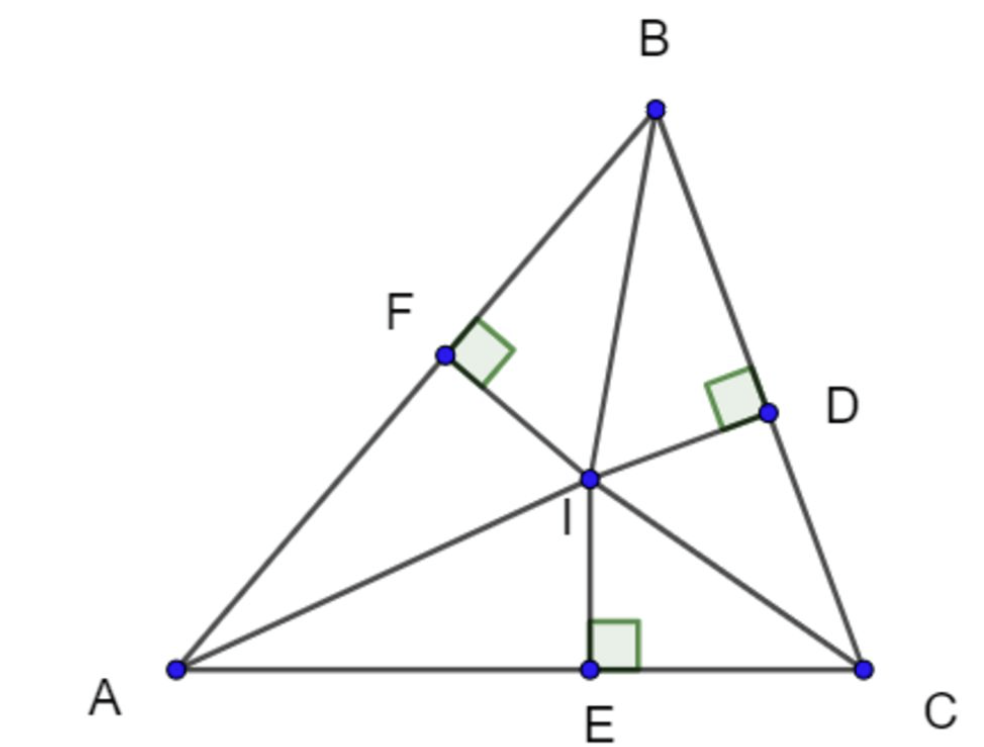
Câu 15: Cho tam giác ABC có BAC = 50°, ACB = 70°. Điểm I nằm trong tam giác thoả mãn góc IAB = 25°, góc ICB = 35°.

a) Chứng minh rằng tia CI là tia phân giác của góc ACB.

Lời giải:

Tính góc ABC:

Trong tam giác ABC, ta có: BAC + ABC + ACB = 180°

Suy ra: ABC = 180° - 50° - 70° = 60°

Tính góc IAC và góc IBC:

IAC = BAC - IAB = 50° - 25° = 25°

IBC = ABC - ICB = 60° - 35° = 25°

Xét tam giác AIC và tam giác BIC:

Ta có: ICB = ICA = 35° (theo đề bài)

Vậy, CI là tia phân giác của góc ACB.

b) Gọi D, E, F lần lượt là hình chiếu vuông góc của I lên các đường thẳng BC, CA, AB. Chứng minh rằng I là giao điểm của ba đường trung trực của tam giác DEF.

Lời giải:

Xét tứ giác AEIF:

Ta có: AEI = AFI = 90°

Suy ra: AEIF là tứ giác nội tiếp.

Do đó: AIE = AFE (cùng chắn cung AE)

Xét tứ giác BFID:

Ta có: BDI = BFI = 90°

Suy ra: BFID là tứ giác nội tiếp.

Do đó: BID = BFD (cùng chắn cung BD)

Xét tứ giác CEID:

Ta có: CDI = CEI = 90°

Suy ra: CEID là tứ giác nội tiếp.

Do đó: CID = CED (cùng chắn cung CD)

Chứng minh I là giao điểm của ba đường trung trực:

Ta có: AIE = 90° - IAE = 90° - 25° = 65°

Tương tự: BID = 90° - IBD = 90° - 25° = 65°

Suy ra: AIE = BID => AFE = BFD

Mà: AFE + BFD = 180° (kề bù)

Suy ra: AFE = BFD = 90°

Vậy, IF ⊥ DE. Tương tự, ta chứng minh được IE ⊥ DF và ID ⊥ EF.

Do đó, I là giao điểm của ba đường trung trực của tam giác DEF.

Kết luận:

a) Tia CI là tia phân giác của góc ACB.

b) I là giao điểm của ba đường trung trực của tam giác DEF.