Hình vuông - Một trong những dạng hình học mà các em cần phải ghi nhớ. Đây là hình mà các em đã học từ cấp 1, tuy nhiên đến cấp 2, những kiến thức về hình vuông sẽ được mở rộng.
Cùng Admin tổng hợp lại lý thuyết và một số bài tập vận dụng về hình vuông trong Toán 9 qua bài chia sẻ dưới đây nhé.
A. Lý thuyết
Ở phần đầu này, Admin sẽ đưa lại các lý thuyết có ở Toán 9 về hình vuông để các em ghi nhớ nhé!
1. Định nghĩa
Hình vuông là tứ giác có bốn góc vuông và có bốn cạnh bằng nhau.
Hình vuông là gì?
Tổng quát: ABCD là hình vuông khi và chỉ khi
$\widehat{A}=\widehat{B}=\widehat{C}=\widehat{D}=90^{\circ}$ và $AB = BC = CD = DA$
Nhận xét:
- Hình vuông là hình chữ nhật có bốn cạnh bằng nhau.
- Hình vuông là hình thoi có bốn góc vuông.
- Hình vuông vừa là hình chữ nhật vừa là hình thoi.
2. Tính chất
Hình vuông có tất cả các tính chất của hình chữ nhật và hình thoi.
3. Dấu hiệu nhận biết hình vuông
Làm cách nào để nhận biết hình vuông. Các em cần phải ghi nhớ các dấu hiệu sau đây:
- Hình chữ nhật có hai cạnh kề bằng nhau là hình vuông.
- Hình chữ nhật có hai đường chéo vuông góc với nhau là hình vuông.
- Hình chữ nhật có một đường chéo là đường phân giác một góc là hình vuông.
- Hình thoi có một góc vuông là hình vuông.
- Hình thoi có hai đường chéo bằng nhau là hình vuông.
Cần ghi nhớ dấu hiệu nhận biết hình vuông
Ví dụ: Cho tam giác ABC vuông tại A. Phân giác trong AD của góc A (D ∈ BC ). Vẽ DF ⊥ AC, DE ⊥ AB. Chứng minh tứ giác AEDF là hình vuông.
Hướng dẫn:
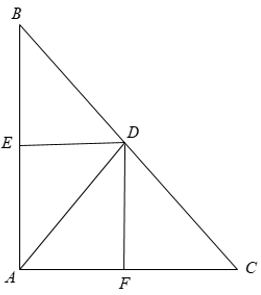
+ Xét tứ giác AEDF có
$\widehat{A}=\widehat{E}=\widehat{F}=90^{\circ}$
⇒ AEDF là hình chữ nhật . ( 1 )
Theo giả thiết ta có AD là đường phân giác của góc $\widehat{A}$
⇒ $\widehat{EAD} = \widehat{DAF} = 45^{\circ}$
+ Xét Δ AED có:
$\widehat{AED} = 90^{\circ}$; $\widehat{DAE} = 45^{\circ}$ ⇒ $\widehat{EDA} = 45^{\circ}$
⇒ Δ AED vuông cân tại E nên AE = ED ( 2 )
Từ ( 1 ),( 2 ) ⇒ AEDF là hình vuông (dấu hiệu 1 – mục 3)
B. Bài tập vận dụng
Bài 1: Cho hình vuông ABCD. Gọi I,K lần lượt là trung điểm của AD và DC.
a) Chứng minh rằng BI ⊥ AK.
b) Gọi E là giao điểm của BI và AK. Chứng minh rằng CE = AB.
Hướng dẫn:

Xét Δ BAI và Δ ADK có:
$AB=AD \\ AI=DK=\frac{1}{2}AB =\frac{1}{2}DA$
$\widehat{A}=\widehat{D}=90^{\circ}$
⇒ Δ BAI = Δ ADK ( c - g - c )
⇒ $\widehat{ABI} = \widehat{DAK}$ (góc tương ứng bằng nhau)
Mà $\widehat{IAE} + \widehat{EAB} = 90^{\circ}$ ⇒ $\widehat{ABI} + \widehat{EAB} = 90^{\circ}$
+ Xét Δ ABE có $\widehat{EAB} + \widehat{ABE} +\widehat{AEB} = 180^{\circ}$
⇒ $\widehat{AEB} = 180^{\circ} - (\widehat{ABE} + \widehat{BAE}) = 180^{\circ} -90^{\circ} = 90^{\circ}$
hay AK ⊥ BI (đpcm)
+ Xét tứ giác EBCK có: $\widehat{KEB} + \widehat{EBC} + \widehat{BCK}+ \widehat{CKE} = 360^{\circ}$
⇒ $\widehat{EBC} + \widehat{EKC} = 180^{\circ}$.
Mà: $\widehat{AKD} + \widehat{AKC} = 180^{\circ}$ nên $\widehat{EBC}= \widehat{EKD}$
+ Tứ giác EBCK nội tiếp nên $\widehat{BEC} = \widehat{BKC}$
Mà $\widehat{BKC} = \widehat{AKD}$ nên $\widehat{EBC} = \widehat{BEC}$ hay tam giác BEC cân tại C
⇒ CE = BC = AB (đpcm)
Bài 2: Cho hình vuông ABCD cạnh bằng a. Trên hai cạnh BC, CD lấy lần lượt hai điểm M, N sao cho $\widehat{MAN} = 45^{\circ}$. Trên tia đối của của tia DC lấy điểm K sao cho DK = BM. Hãy tính :
a) Tính số đo $\widehat{KAN}$= ?
b) Chu vi tam giác MCN theo a.
Hướng dẫn:
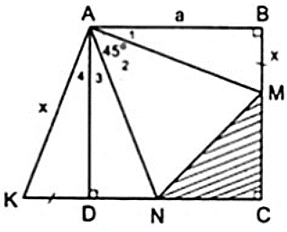
a) Áp dụng định nghĩa và giả thiết của hình vuông ABCD, ta được
$\widehat{B}=\widehat{D}=90^{\circ} \\ A B=A D, B M=D K.$
⇒ Δ ABM = Δ ADK ( c - g - c )
Áp dụng kết quả của hai tam giác bằng nhau và giả thiết, ta có:
$\widehat{A_1}+\widehat{A_2}+\widehat{A_3}=90^{\circ} \\ \widehat{A_1}=\widehat{A_4} ; \widehat{A_2}=45^{\circ}.$
⇒ $\widehat{KAN} = \widehat{A_3}+ \widehat{A_4}= \widehat{A_1}+ \widehat{A_3}= 90^{\circ} - 45^{\circ}= 45^{\circ}$
b) Đặt BM = DK = x thì KN = x + DN, MC = a - x, CN = a - DN
Từ kết quả của hai tam giác bằng nhau ở câu a và giả thiết ta có:
$A M=A K, A N=A N \\ \widehat{M A N}=\widehat{K A N}=45^{\circ}.$
⇒ Δ AMN = Δ AKN ( c - g - c )
⇒ MN = KN (cạnh tương ứng bằng nhau)
Khi đó, chu vi của tam giác MCN là
MC + CN + MN = a - x + a - DN + x + DN = 2a.
C. Đề trắc nghiệm
Tiếp theo đây, hãy thử vận dụng các kiến thức về hình học và những thông tin hình vuông được Admin chia sẻ để làm thử đề 20 câu hỏi trắc nghiệm dưới đây nhé!
Bài 1: Hình vuông là tứ giác có
A. Có bốn cạnh bằng nhau
B. Có bốn góc bằng nhau
C. Có 4 góc vuông và bốn cạnh bằng nhau
D. Cả A, B, C đều sai
=> Đáp án:
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Chọn là: C
Bài 2: Điền cụm từ thích hợp nhất vào chỗ trống: “Tứ giác có 4 cạnh bằng nhau và 4 góc bằng nhau là …”
A. Hình vuông
B. Hình chữ nhật
C. Hình bình hành
D. Hình thoi
=> Đáp án:
Hình vuông là tứ giác có bốn góc vuông và bốn cạnh bằng nhau.
Chọn là: A
Bài 3: Khẳng định nào sau đây là sai?
A. Hình vuông vừa là hình thoi vừa là hình chữ nhật
B. Hình vuông là hình chữ nhật nhưng không là hình thoi
C. Hình vuông có hai đường chéo bằng nhau và vuông góc với nhau
D. Hình vuông có đường chéo là phân giác các góc trong hình vuông
=> Đáp án:
Hình vuông vừa là hình chữ nhật và hình thoi nên nó có đầy đủ tính chất của hình chữ nhật và hình thoi.
Từ đó A, C, D đúng, B sai.
Chọn là: B
Bài 4: Nếu ABCD là hình vuông thì:
A. AC = BD
B. AC, BD giao nhau tại trung điểm mỗi đường
C. AC ⊥ BD
D. Cả A, B, C đều đúng
=> Đáp án:
Hình vuông có hai đường chéo bằng nhau, vuông góc với nhau và giao nhau tại trung điểm mỗi đường nên ABCD là hình vuông thì AC = BD, AC ⊥ BD, AC và BD giao nhau tại trung điểm mỗi đường.
Chọn là: D
Bài 5: Hãy chọn câu đúng. Cho hình vẽ. Tứ giác là hình vuông theo dấu hiệu:
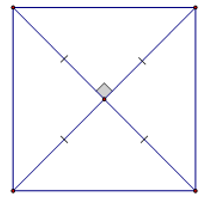
A. Hình thoi có một góc vuông
B. Tứ giác có hai đường chéo bằng nhau
C. Hình bình hành có hai đường chéo bằng nhau
D. Hình thoi có hai đường chéo bằng nhau
=> Đáp án:
Từ hình vẽ ta thấy hai đường chéo của tứ giác vuông góc và giao nhau tại trung điểm mỗi đường nên nó là hình thoi.
Hình thoi này có hai đường chéo bằng nhau nên nó là hình vuông.
Chọn là: D
Bài 6: Hãy chọn câu đúng. Cho hình vẽ. Tứ giác là hình vuông theo dấu hiệu:
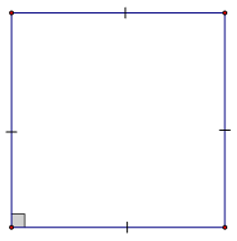
A. Hình thoi có một góc vuông
B. Tứ giác có hai đường chéo bằng nhau
C. Hình bình hành có hai đường chéo bằng nhau
D. Hình thoi có hai đường chéo bằng nhau
=> Đáp án:
Từ hình vẽ ta thấy bốn cạnh của tứ giác này bằng nhau nên tứ giác này là hình thoi.
Hình thoi này có một góc vuông nên nó là hình vuông.
Chọn là: A.
Bài 7: Chọn câu trả lời đúng. Tứ giác nào có hai đường chéo vuông góc với nhau?
A. Hình thoi
B. Hình vuông
C. Hình chữ nhật
D. Cả A và B
=> Đáp án:
Hình thoi và hình vuông đều có hai đường chéo vuông góc với nhau.
Chọn là: D
Bài 8: Chọn câu sai. Tứ giác nào có hai đường chéo bằng nhau.
A. Hình vuông
B. Hình thang cân
C. Hình chữ nhật
D. Hình thoi
=> Đáp án
Trong các hình: hình vuông, hình chữ nhật, hình thang cân, hình thoi thì hình thoi là hình có hai đường chéo không bằng nhau.
Chọn D
Bài 9: Cho hình vuông ABCD. Trên các cạnh AB, BC, CD, DA lần lượt lấy các điểm E, F, G, H sao cho AE = BF = CG = DH sao cho AE = BF = CG = DH. Tứ giác EFGH là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình vuông
=> Đáp án:
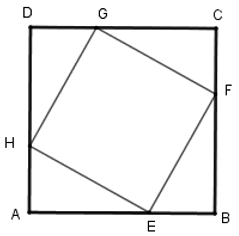
Vì ABCD là hình vuông nên AB = BC = CD = DA (tính chất).
Mà AE = BF = CG = DH (gt) nên AB – AE = BC – BF = CD – CG = DA – DH hay DG = CF = EB = AH
Từ đó suy ra ΔAHE = ΔDGH = ΔCFG = ΔEBF (c-g-c) nên HG = GF = HE = EF.
Vì HG = GF = HE = EF nên tứ giác EFGH là hình thoi.
Vì ΔAHE = ΔBEF (cmt)
$\Rightarrow \widehat{AHE}=\widehat{BEF}$ (hai góc tương ứng)
Mà $\widehat{AHE}+\widehat{HEA}=90^{\circ}$
$\Rightarrow \widehat{BEF}+\widehat{HEA}=90^{\circ}$
Từ đó $\widehat{HEF}=180^{\circ}-(\widehat{HEA}+\widehat{BEF})$
$=180^{\circ}-90^{\circ}$
$=90^{\circ}$
Hình thoi EFGH có góc HEF = $=90^{\circ}$ nên EFGH là hình vuông.
Chọn D
Bài 10: Cho hình thoi ABCD, O là giao điểm của hai đường chéo. Các tia phân giác 4 góc đỉnh O cắt các cạnh AB, BC, CD, DA theo thứ tự ở E, F, G, H. Tứ giác EFGH là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình vuông
=> Đáp án:
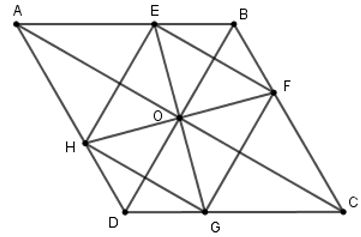
Vì ABCD là hình thoi nên AC ⊥ BD; OA = OC; OB = OD (tính chất).
Mà OE; OF; OG; OH lần lượt là phân giác góc AB, BOC, DOG, AOD nên ta có:
$\widehat{EOB}=\widehat{OHA}=\widehat{BOF}=45^{\circ}$
$\Rightarrow \widehat{HOA}+\widehat{AOB}+\widehat{BOF}=45^{\circ}+90^{\circ}+45^{\circ}= 180^{\circ}$
$\Rightarrow H, O, F$ thẳng hàng.
Tương tự ta có: $E, O,G$ thẳng hàng.
Xét $\triangle O E B$ và $\triangle O G D$ ta có:
$OD=OB ; \widehat{EOB} =\widehat{GOD} \text { (đối đỉnh); } \widehat{EBO} =\widehat{ODG} \text { (so le trong) }$
$\Rightarrow \triangle {OEB} =\triangle{OGD}$ (g-c-g)
$\Rightarrow OE =OG (1)$
Tương tự ta có: ΔOFB = ΔOHD (g – c – g)
⇒ OF = OH (2)
Từ (1) và (2) suy ra: tứ giác EFGH là hình bình hành vì có hai đường chéo EG; HF giao nhau tại trung điểm mỗi đường.
Lại xét ΔOEB và ΔOFB có:
$\widehat{EBO}=\widehat{FBO} \text { (do } BO \text { là phân giác } \widehat{ABC})$
$OB \text { chung }$
$\widehat{EOB}=\widehat{BOF}=45^{\circ}$
Nên ΔOEB = ΔOFB (g – c – g) ⇒ OE = OF ⇒ 2 OE = 2 OF hay EG = HF
$\Rightarrow$ Hình bình hành EFGH có hai đường chéo bằng nhau EG = HF nên EFGH là hình chữ nhật.
Lại có: $\widehat{EOB}+\widehat{BOF}=45^{\circ}+45^{\circ}=90^{\circ}$
$\Rightarrow \widehat{EOF}=90^{\circ} \Rightarrow EG \perp FH$
Hình chữ nhật EFGH có: EG ⊥ HF nên EFGH là hình vuông.
Chọn D
Bài 11: Cho hình vuông có chu vi 28 cm. Độ dài cạnh hình vuông là:
A. 4cm
B. 7 cm
C. 14 cm
D. 8 cm
=> Đáp án:
Hình vuông có 4 cạnh bằng nhau nên chu vi hình vuông bằng 4a. (a là độ dài một cạnh)
Từ giả thiết ta có 4a = 28 ⇔ a = 7cm.
Vậy cạnh hình vuông là a = 7cm
Chọn B
Bài 12: Cho hình vuông có chu vi 32 cm. Độ dài cạnh hình vuông là:
A. 10cm
B. 15 cm
C. 5 cm
D. 8 cm
=> Đáp án:
Hình vuông có 4 cạnh bằng nhau nên chu vi hình vuông bằng 4a. (a là độ dài một cạnh)
Từ giả thiết ta có 4a = 32 ⇔ a = 8cm.
Vậy cạnh hình vuông là a = 8cm
Chọn D
Bài 13: Cho hình vuông có chu vi 16 cm. Bình phương độ dài một đường chéo của hình vuông là:
A. 32
B. 16
C. 24
D. 18
=> Đáp án:
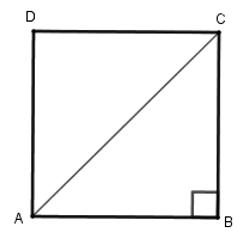
Gọi hình vuông ABCD có chu vi là 16cm. Khi đó 4.AB = 16cm
⇒ AB = 4cm = AB = CD = DA
Xét tam giác ABC vuông tại B, theo định lý Pytago ta có
AB2 + BC2 = AC2 ⇒ AC2 = 42 + 42 ⇔ AC2 = 32
Vậy bình phương độ dài một đường chéo là: 32
Chọn A
Bài 14: Cho hình vuông có chu vi 20 cm. Bình phương độ dài một đường chéo của hình vuông là:
A. 32
B. 50
C. 25
D. 30
=> Đáp án:
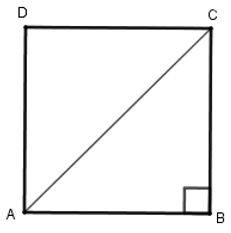
Gọi hình vuông ABCD có chu vi là 20cm. Khi đó 4.AB = 20cm
⇒ AB = 5cm = AB = CD = DA
Xét tam giác ABC vuông tại B, theo định lý Pytago ta có
AB2 + BC2 = AC2 ⇒ AC2 = 52 + 52 ⇔ AC2 = 50
Vậy bình phương độ dài một đường chéo là: 50
Chọn B
Bài 15: Cho tứ giác ABCD. Gọi E, F, G, H theo thứ tự là trung điểm của AB, BC, CD, DA. Tìm điều kiện của tứ giác ABCD để hình bình hành EFGH là hình vuông.
A. BD ⊥ AC; BD = AC
B. BD ⊥ AC
C. BD = AC
D. AC = BD và AB // CD
=> Đáp án:
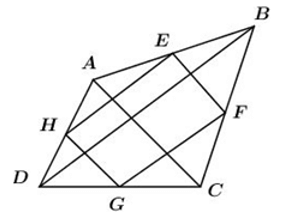
Ta có EH; EF lần lượt là đường trung bình của tam giác ABD; BAC nên (1)
$E H / / B D ; E F / / A C$
$E H=\frac{1}{2} B D ; E F=\frac{1}{2} A C.$
Hình bình hành EFGH là hình vuông khi và chỉ khi
(2) $E H \perp E F \\ E H=E F.$
Từ (1); (2) ⇒ $B D \perp A C ; D B=A C.$
thì hình bình hành EFGH là hình vuông
Chọn A
Bài 16: Cho hình vuông ABCD. M là điểm nằm trong hình vuông. Gọi E, F lần lượt là hình chiếu của M trên cạnh AB và AD. Tứ giác AEMF là hình vuông khi.
A. M trên đường chéo AC
B. M thuộc cạnh DC
C. M thuộc đường chéo BD
D. M tùy ý nằm trong hình vuông ABCD
=> Đáp án:
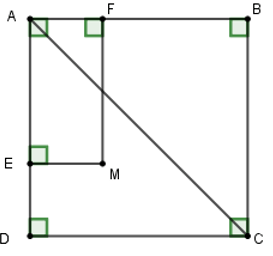
Tứ giác AFME có: $\widehat{A}=\widehat{AFM}=\widehat{AEM}=90^{\circ}$ nên AEMF là hình chữ nhật
Để hình chữ nhật AEMF là hình vuông thì AM là phân giác $\widehat{E A F}$
Mà ta lại có: AC là phân giác góc DAB (do ABCD là hình vuông)
Nên suy ra M ∈ AC.
Chọn A
Bài 17: Cho hình vuông ABCD. M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA. Hãy chọn câu đúng.
A. $S_{M N P Q}=\frac{1}{3} S_{A B C D}$
B. $S_{M N P Q}=\frac{1}{4} S_{A B C D}$
C. $S_{M N P Q}=\frac{1}{2} S_{A B C D}$
D. $S_{M N P Q}=\frac{2}{3} S_{A B C D}$
=> Đáp án:
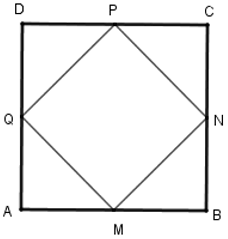
Gọi cạnh của hình vuông ABCD là a.
Vì ABCD là hình vuông là M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA nên ta có AM = MB = BN = NC = CP = PD = DQ = QA = a/2
Từ đó: ΔAQM = ΔBMN = ΔCPN = ΔDQP (c – g – c)
$ \Rightarrow S_{Q A M} =S_{M N B}=S_{C P N}=S_{D P Q}$
$=\frac{D Q \cdot D P}{2}=\frac{\frac{a}{2} \cdot \frac{a}{2}}{2}=\frac{a^2}{4.2}=\frac{a^2}{8}$
Lại có SABCD = a2.
Nên SMNPQ = SABCD – SAMQ – SMBN – SCPN – SDPQ = $a^2-4 \cdot \frac{a^2}{8}=\frac{1}{2} a^2=\frac{1}{2} S_{ABCD}$
Vậy SMNPQ = ½ SABCD.
Chọn C
Bài 18: Cho hình vuông ABCD cạnh 8 cm. M, N, P, Q là trung điểm các cạnh AB, BC, CD, DA. Tính diện tích tứ giác MNPQ.
A. SMNPQ = 28 cm2
B. SMNPQ = 30cm2
C. SMNPQ = 16cm2
D. SMNPQ = 32cm2
=> Đáp án;
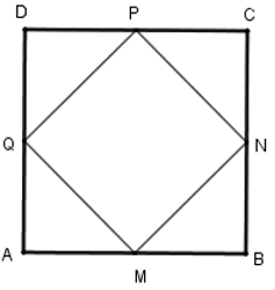
Vì ABCD là hình vuông và M, N, P, Q là trung điểm các cạnh AB, BC, CD, CA nên ta có AM = MB = BN = NC = CP = PD = DQ = QA = 8/2 = 4 cm
Từ đó: ΔAQM = ΔBMN = ΔCPN = ΔDQP (c – g – c)
Suy ra
$S_{Q A M}=S_{\triangle A B}=S_{C P N}=S_{D P Q}=\frac{D Q \cdot D P}{2}=\frac{8^2}{8}=8$
Lại có SABCD = 82 = 64.
Nên $S_{MNPQ} = S_{ABCD} – S_{AMQ} – S_{MBN} – S_{CPN} – S_{DPQ} = 32$
Vậy SMNPQ = 32 cm2.
Chọn D
Bài 19: Cho tam giác ABC vuông tại A. Gọi M, N, P lần lượt là các trung điểm của AB, BC, AC. Tam giác ABC cần có thêm điều kiện gì để hình chữ nhật AMNP là hình vuông?
A. AB = ½ AC
B. AB = AC
C. AC = ½ AB
D. Góc B $=60^{\circ}$
=> Đáp án:
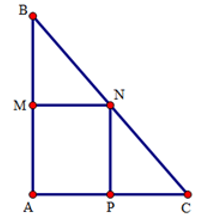
Hình chữ nhật AMNP là hình vuông ⇔ AM = AP
Mà AM = ½ AB; AP = ½ AC (gt) nên AM = AP ⇔ AB = AC
Vậy nếu tam giác ABC vuông cân tại A thì hình chữ nhật AMNP là hình vuông.
Chọn B
Bài 20: Cho tam giác ABC vuông cân tại A. Trên cạnh BC lấy các điểm H, G sao cho BH = HG = GC. Qua H và G kẻ các đường vuông góc với BC, chúng cắt AB và AC theo thứ tự tại E và F. Tứ giác EFGH là hình gì?
A. Hình chữ nhật
B. Hình thoi
C. Hình bình hành
D. Hình vuông
=> Đáp án:
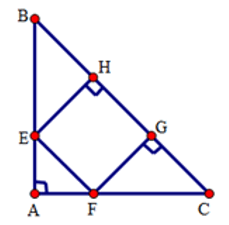
Ta có: $\triangle{ABC}$ vuông cân tại $A$ nên:
$\widehat{B}=\widehat{C}=\frac{180^{\circ}-A}{2}=\frac{180^{\circ}-90^{\circ}}{2}=45^{\circ}$
Xét tam giác vuông FGC có:
$\widehat{GFC} = 180^{\circ}-\widehat{FGC}-\widehat{C}$
$=180^{\circ}-90^{\circ}-45^{\circ} =45^{\circ}$
$\Rightarrow \widehat{GFC}=\widehat{C}$
Suy ra ΔFGC là tam giác vuông cân tại G ⇒ FG = GC
Chứng minh tương tự:
Xét tam giác vuông EHB có:
$\widehat{BEH} =180^{\circ}-\widehat{EHB}-\widehat{B}$
$ =180^{\circ}-90^{\circ}-45^{\circ}=45^{\circ}$
$\Rightarrow \widehat{BEH} =\widehat{B}$
Suy ra tam giác EBH vuông cân tại H ⇒ EH = HB
Mà BH = HG = GC (gt) nên FG = EH = HG
Lại có:
$E H = F G(c m t); E H / / F G (cmt)$
⇒ EFGH là hình bình hành (dhnb)
Mà góc $H=90^{\circ}$ (do EH ⊥ BC) nên hình bình hành EFGH là hình chữ nhật
Mặt khác EH = HG (cmt) nên hình chữ nhật EFGH là hình vuông.
Đáp án cần chọn là: D
Và bây giờ, hãy cùng so đáp án và cho Admin biết các em đúng được bao nhiêu câu với 20 đề trắc nghiệm ở trên nhé. Nếu đạt 20/20, vậy thì chúc mừng, các em đã nắm rất kỹ các kiến thức về hình vuông và tính chất của nó rồi nhé!



















![Top 15 trường THPT tư thục tốt nhất TPHCM [Cập nhật mới 2023]](https://static.fqa.vn/fqa/sgk/top_truong_thpt_tu_thuc_tot_nhat_tphcm_be9958a086.jpg)





