[Kiến thức toán 11] Công thức cấp số cộng + Bài tập vận dụng

Công thức cấp số cộng chuẩn xác tính như thế nào? Bài viết này Admin sẽ cùng các em ôn lại toàn bộ kiến thức và một số bài tập vận dụng cơ bản. Đọc và bổ sung kiến thức để cùng Admin học toán giỏi hơn mỗi ngày nhé!

Định nghĩa và công thức cấp số cộng

Một cấp số cộng là dãy số thỏa mãn điều kiện hai phân tử kế tiếp nhau cách nhau bằng 1 hằng số. 

Ví dụ: Dãy cấp số cộng 3, 5, 7, 9, 11,... : hai số hạng liên tiếp nhau cách nhau 2 đơn vị.

Cho dãy số $u_n$ là một cấp số cộng, nếu nó thỏa mãn điều kiện sau:

$u_{n+1}=u_n+d$ (n ∊ N*, d là hằng số) 

Cấp số cộng

Công sai của cấp số cộng

Trong một cấp số cộng, d là hằng số hay còn gọi là công sai của cấp số cộng. Cách tính công sai với công thức sau:

$d=u_{n+1}-u_n$ (Nếu d = 0 thì cấp số cộng là một dãy số không đổi)

Ví dụ: Cho một dãy số: 3, 6, 9, 12, 15, 18. Đây có phải là một cấp số cộng hay không?

Giải:

Ta có: 

6 = 3 + 3

9 = 6 + 3

12 = 9 + 3

15 = 12 + 3

18 = 15 + 3

=> Dãy số 3, 6, 9, 12, 15, 18 là một cấp số cộng với công sai d = 3 và số hạng đầu là $u_1=3$

Số hạng tổng quát

Số hạng tổng quát $u_n$ sẽ được tính bằng công thức sau:

$u_n=u_1 + (n-1) \cdot d$ (n ≥ 2, n là số tự nhiên bất kỳ > 1)

=> Công sai của cấp số cộng sẽ được tính bằng công thức:

$d=\frac{u_n-u_1}{n-1}$

Ví dụ: Cho cấp số cộng $u_n$, biết $u_n$ = - 1, d = 3. Hãy tính $u_20$?

Giải:

Áp dụng công thức tìm số hạng tổng quát cho cấp số cộng, ta có:

$u_n$ = $u_1$ + (n-1).d

=> $u_20$ = (-1) + (20-1).3 = 56.

Vậy $u_20$  = 56.

Tính chất cấp số cộng

Nếu $u_n$ là một cấp số cộng, bắt đầu từ số hạng thứ 2, mỗi số hạng đều là trung bình cộng của 2 số hạng đứng kề trước và kề sau nó trong dãy. Công thức tổng quát như sau:

$u_k=\frac{u_{k-1}+u_{k+1}}{2}$ với $k \geq 2$ hay $u_{k+1}+u_{k-1}=2 u_k$

Ví dụ: Cho ba số  2, x, 6 theo thứ tự lập thành một cấp số công. Hãy tìm x. 

Giải:

Áp dụng công thức:$u_k=\frac{u_{k-1}+u_{k+1}}{2} = \frac{2 + 6}{2} = 4$

Vậy, x có giá trị cần tìm là 4.

Tổng n số hạng đầu

Tổng n số hạng đầu của 1 cấp số cộng được gọi là tổng riêng thứ n. Công thức tính tổng n số hạng đầu như sau:

Tính tổng n số hạng đầu qua số hạng đầu, cuối và số số hạng:

$S_n=n u_1+\frac{n(n-1)}{2} d, \left(với n \in N^*\right)$

Tính tổng n số hạng đầu qua số hạng đầu, số số hạng và công sai:

$S_n=n u_1+\frac{n(n-1)}{2} d$

=> $S_n=\frac{n\left[2 u_1+(n-1) d\right]}{2}$

Ví dụ: Cho cấp số cộng $u_n$ với $u_1$ = - 1 và d = 3. Hãy tính tổng 20 số hạng đầu.

Áp dụng công thức tính tổng n số hạng đầu, ta có:

$S_n=n u_1+\frac{n(n-1)}{2} d$

=> $S_{20}=20. (-1) +\frac{20.(20-1)}{2}. 3 = 550$

Vậy tổng 20 số hạng đầu $S_{20}$ là 550.

Bài tập cấp số cộng vận dụng công thức

Sau khi các em đã nắm rõ và đầy đủ các công thức cấp số cộng, bây giờ hãy vận dụng nó vào giải một số bài tập sau:

Bài 1: Cho một cấp số cộng $u_n$ với $u_1$ = 5, $u_2$ = 10. Tìm giá trị công sai của cấp số cộng đã cho.

Giải:

Số hạng tổng quát của cấp số cộng $u_n$ là: $u_n$ = $u_1$ + (n-1).d

Trong công thức tổng quát trên, $u_1$ chính là số hạng đầu của dãy, d là công sai.

=> $u_2$ =$u_1$ + d 

⇔ 10 = 5 + d 

=> d = 5

Vậy, công sai d của cấp số cộng $u_n$ là 5.

Bài 2: Cho một cấp số cộng $u_n$, biết $u_1$ = - 3, $u_6$ = 27. Hãy tính giá trị công sai d của cấp số cộng $u_n$?

Giải:

Biến đổi từ công thức cấp số cộng, ta có:

$u_6$= 27 

⇔ $u_1$ + 5.d = 27

⇔ 5.d = 27 + 3 

⇔ d = 6

Vậy, giá trị công sai d của cấp số cộng $u_n$ là 6.

Bài 3: Tìm 4 số hạng liên tiếp của một cấp số cộng có tổng của 4 số hạng là 20 và tổng các bình phương của 4 số bằng 120.

Giải:

Giả sử, 4 số hạng liên tiếp trong dãy cấp số cộng lần lượt là: a - 3x, a - x, a + x và a + 3x  và công sai d = 2x. Khi đó, ta có hệ phương trình:

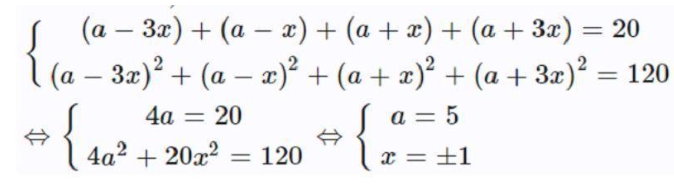
Cách giải bài 3

Như vậy, 4 số hạng liên tiếp trong cấp số cộng cần tìm là: 2, 4, 6, 8.

Bài 4: Tính giá trị x để 3 số 1+ 3x, $x^2$ + 5 và 1 - x theo thứ tự đó lập thành một cấp số cộng

Giải: 

3 số liên tiếp 1+ 3x, $x^2$ + 5 và 1 - x là một cấp số cộng khi:

($x^2$ + 5) - (1+ 3x) = (1 - x ) - ($x^2$ + 5)

⇔ $x^2$ - 3x + 4 = - $x^2$ - x - 4

⇔ $2x^2$ - 2x + 8 = 0 

=> Phương trình vô nghiệm.

Vậy, dãy 3 số 1+ 3x, $x^2$ + 5 và 1 - x không phải là cấp số cộng.

Như vậy, toàn bộ bài viết này Admin đã giúp các em ôn lại tất cả các kiến thức về công thức cấp số cộng. Hy vọng chúng bổ ích và giúp các em giải toán dễ dàng hơn. Có bất kỳ khó khăn hay thắc mắc nào, hãy để lại bình luận dưới bài viết, Admin sẽ sớm hỗ trợ các em nhé!