cho hình chóp đều s.ABC có cạnh đáy bằng a cạnh bên bằng 2a xác định tâm và tính diện tích thể tích mặt cầu ngoại tiếp
Làm sao để có câu trả lời hay nhất?
- Luôn có GIẢI THÍCH các bước giải
- Không copy câu trả lời của Timi
- Không sao chép trên mạng
- Không spam câu trả lời để nhận điểm
- Spam sẽ bị khóa tài khoản



17/12/2023
 0
0
17/12/2023
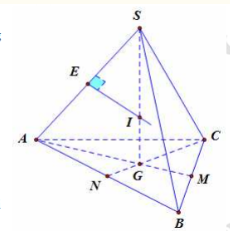
Hình chóp đều có chân đường cao kẻ từ S trùng với tâm đường tròn ngoại tiếp đáy.
Gọi G là trọng tâm tam giác ABC
⟹SG
Gọi M là trung điểm BC
⟹
Gọi E là trung điểm của SA, qua E kẻ Ex
Khi đó: SI=IA=IB=IC=R là bán kính đường tròn ngoại tiếp khối chóp S.ABC
Xét tam giác SAG, có:
Diện tích mặt cầu ngoại tiếp là:
Thể tích mặt cầu ngoại tiếp là:
 0
0
17/12/2023
Để xác định tâm của hình chóp đều, ta vẽ đường thẳng nối tâm của đáy với tâm của mặt cầu ngoại tiếp. Đường thẳng này sẽ đi qua đỉnh của hình chóp và cắt đáy tại tâm của đáy. Do đó, ta có thể xác định tâm của hình chóp bằng cách tìm tâm của đáy.
Vì hình chóp đều, nên tâm của đáy cũng chính là tâm của hình chóp. Do đó, tâm của hình chóp đều sẽ nằm trên đường thẳng nối tâm của đáy với tâm của mặt cầu ngoại tiếp.
Để tính diện tích bề mặt của hình chóp đều, ta sử dụng công thức:
Diện tích bề mặt hình chóp đều = diện tích đáy + diện tích các mặt bên.
Diện tích đáy hình chóp đều là diện tích tam giác đều ABC, có công thức:
Diện tích đáy = (cạnh đáy)^2 * √3 / 4 = a^2 * √3 / 4.
Diện tích các mặt bên của hình chóp đều là các tam giác đều, có cùng diện tích với diện tích đáy, nên diện tích các mặt bên là: diện tích đáy * số mặt bên = (a^2 * √3 / 4) * 4 = a^2 * √3.
Vậy diện tích bề mặt của hình chóp đều sẽ là: a^2 * √3 / 4 + a^2 * √3 = a^2 * √3 * (1/4 + 1) = a^2 * √3 * 5/4.
Để tính thể tích của hình chóp đều, ta sử dụng công thức:
Thể tích hình chóp đều = (diện tích đáy * chiều cao) / 3.
Vì hình chóp đều, nên chiều cao của hình chóp cũng chính là đường cao của tam giác đều ABC. Đường cao của tam giác đều có công thức: đường cao = cạnh đáy * √3 / 2 = a * √3 / 2.
Thay vào công thức thể tích, ta có:
Thể tích hình chóp đều = (a^2 * √3 / 4 * (a * √3 / 2)) / 3 = a^3 * √3 / 12.
Để tính diện tích mặt cầu ngoại tiếp, ta sử dụng công thức:
Diện tích mặt cầu ngoại tiếp = 4πR^2.
Trong đó, R là bán kính của mặt cầu ngoại tiếp.
Do hình chóp đều, nên tâm của mặt cầu ngoại tiếp nằm trên đường thẳng nối tâm của đáy với tâm của mặt cầu ngoại tiếp. Vì vậy, tâm của mặt cầu ngoại tiếp cũng chính là tâm của hình chóp. Do đó, R sẽ bằng khoảng cách từ tâm của hình chóp đến một trong các đỉnh của đáy.
Khoảng cách từ tâm của hình chóp đến đỉnh của đáy là chiều cao của hình chóp, tức là a * √3 / 2.
Thay vào công thức diện tích mặt cầu ngoại tiếp, ta có:
Diện tích mặt cầu ngoại tiếp = 4π * (a * √3 / 2)^2 = 4π * 3a^2 / 4 = 3πa^2.
Vậy diện tích thể tích mặt cầu ngoại tiếp là 3πa^2.
mik ns dị bn hỉu hong
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
1 giờ trước
1 giờ trước
Top thành viên trả lời




 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




