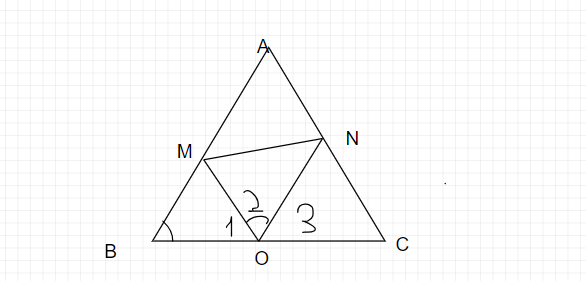
Cho tam giác ABC cân tại A , góc A < 90° O thuộc cạch BC . Trên cạnh AB,AC lần lượt lấy 2 điểm MN , sao cho góc MON = góc ABC. C/m tam giác BMO đồng dạng tam giác CON

1. Đây là một bài toán về tam giác và đồng dạng tam giác. Chúng ta cần chứng minh rằng tam giác BMO đồng dạng tam giác CON. Cách giải: Bước 1: Vẽ đồ thị để hiểu rõ hơn về bài toán. Bước 2: Sử dụng các thông tin đã cho và các tính chất của tam giác để chứng minh đồng dạng tam giác. 2. Giải bài toán: Bước 1: Vẽ đồ thị: \[ \begin{tikzpicture} \draw (0,0) -- (4,0) -- (2,3) -- cycle; \draw (2,3) -- (1,0); \draw (2,3) -- (3,0); \node at (0,0) [below] {B}; \node at (4,0) [below] {C}; \node at (2,3) [above] {A}; \node at (1,0) [below] {M}; \node at (3,0) [below] {N}; \node at (2,0) [below] {O}; \end{tikzpicture} \] Bước 2: Chứng minh đồng dạng tam giác BMO và CON. Ta có góc A = góc BAC (vì tam giác ABC cân tại A) Và góc MON = góc ABC (theo đề bài) Do đó, ta có: \[ \angle BMO = \angle BMA + \angle AMO = \angle BAC + \angle MON = \angle BAC + \angle ABC \] \[ \angle CON = \angle CAN + \angle ANO = \angle BAC + \angle MON = \angle BAC + \angle ABC \] Vậy, ta có \(\angle BMO = \angle CON\). Tiếp theo, ta cần chứng minh \(\frac{{BM}}{{CO}} = \frac{{BO}}{{CN}}\) để tam giác BMO đồng dạng tam giác CON. Ta có: \[ \frac{{BM}}{{CO}} = \frac{{BA}}{{CA}} \quad (\text{vì } \triangle BMO \sim \triangle BAC) \] \[ \frac{{BO}}{{CN}} = \frac{{BA}}{{CA}} \quad (\text{vì } \triangle BOC \sim \triangle CAN) \] Vậy, ta có \(\frac{{BM}}{{CO}} = \frac{{BO}}{{CN}}\). Từ đó, ta kết luận được rằng tam giác BMO đồng dạng tam giác CON. Kết luận: Tam giác BMO đồng dạng tam giác CON.