Giúp tôi với

Câu 1. Trước tiên, ta cần hiểu rằng khi diễn viên xiếc đứng cân bằng trên dây, tổng các lực tác dụng lên diễn viên phải bằng không. Các lực này bao gồm lực căng của dây từ hai phía ($$ và $$) và trọng lượng của diễn viên ($$). Ta có: $$ Trọng lượng của diễn viên là 700 N, tức là: $$ Dây võng xuống với góc $$. Điều này có nghĩa là mỗi lực căng của dây tạo với đường thẳng đứng một góc $$ (vì $$, và mỗi bên sẽ là $$). Ta phân tích lực căng của dây thành các thành phần dọc và ngang. Vì diễn viên đứng cân bằng, thành phần ngang của hai lực căng phải bằng nhau và ngược chiều, do đó chúng triệt tiêu lẫn nhau. Thành phần dọc của hai lực căng phải bằng trọng lượng của diễn viên. Ta có: $$ Vì $$, ta có: $$ Giải phương trình này để tìm $$: $$ Sử dụng giá trị của $$: $$ Do đó: $$ Làm tròn đến hàng đơn vị, ta có: $$ Vậy lực căng của dây treo khi diễn viên xiếc đứng cân bằng là: $$ Câu 2. Để tính giá trị của biểu thức $$, ta sẽ dựa vào điều kiện đã cho $$. Bước 1: Ta thấy rằng biểu thức $$ có dạng tương tự với biểu thức đã cho, nhưng hệ số của $$ khác nhau. Do đó, ta sẽ nhân cả hai vế của điều kiện đã cho với 2 để dễ dàng biến đổi: $$ $$ Bước 2: Ta nhận thấy rằng biểu thức $$ có dạng $$. Để biến đổi biểu thức này từ biểu thức đã cho, ta sẽ trừ đi một lần biểu thức $$: $$ $$ $$ Bước 3: Ta nhận thấy rằng biểu thức $$ đã xuất hiện ở điều kiện ban đầu, do đó ta có thể rút gọn biểu thức trên: $$ Bước 4: Bây giờ, ta sẽ lấy biểu thức $$ trừ đi biểu thức $$: $$ $$ Bước 5: Ta nhận thấy rằng biểu thức $$ đã xuất hiện ở điều kiện ban đầu, do đó ta có thể rút gọn biểu thức trên: $$ Bước 6: Ta nhận thấy rằng biểu thức $$ đã xuất hiện ở điều kiện ban đầu, do đó ta có thể rút gọn biểu thức trên: $$ Bước 7: Ta nhận thấy rằng biểu thức $$ đã xuất hiện ở điều kiện ban đầu, do đó ta có thể rút gọn biểu thức trên: $$ Bước 8: Ta nhận thấy rằng biểu thức $$ đã xuất hiện ở điều kiện ban đầu, do đó ta có thể rút gọn biểu thức trên: $$ Bước 9: Ta nhận thấy rằng biểu thức $$ đã xuất hiện ở điều kiện ban đầu, do đó ta có thể rút gọn biểu thức trên: $$ Bước 10: Ta nhận thấy rằng biểu thức $$ đã xuất hiện ở điều kiện ban đầu, do đó ta có thể rút gọn biểu thức trên: $$ Vậy giá trị của biểu thức $$ là: $$ Đáp số: $$ 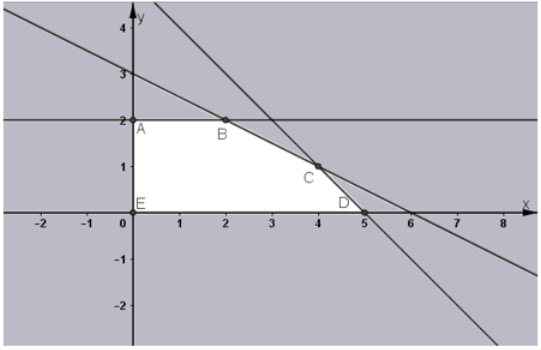Câu 3. Để giải bài toán này, chúng ta sẽ sử dụng phương pháp lập phương trình và tối ưu hóa hàm số. Gọi số đơn vị sản phẩm loại I là $$ và số đơn vị sản phẩm loại II là $$. Từ bảng dữ liệu, ta có các ràng buộc về số máy: - Nhóm A: $$ - Nhóm B: $$ - Nhóm C: $$ Ta cũng có các điều kiện không âm: $$ $$ Hàm mục tiêu là lợi nhuận tổng cộng: $$ Bây giờ, ta sẽ tìm các điểm đỉnh của vùng giải bằng cách giải các phương trình ràng buộc: 1. $$ 2. $$ 3. $$ Từ phương trình thứ hai: $$ Thay vào phương trình thứ nhất: $$ $$ $$ $$ Vậy ta có điểm $$. Thay vào phương trình thứ ba: $$ $$ $$ $$ Vậy ta có điểm $$. Tiếp theo, ta kiểm tra các điểm biên: - $$: - Từ $$: $$ - Từ $$: $$ nên $$ - Vậy ta có điểm $$ và $$. - $$: - Từ $$: $$ nên $$ - Từ $$: $$ nên $$ - Vậy ta có điểm $$ và $$. Tuy nhiên, điểm $$ không thỏa mãn ràng buộc $$. Do đó, ta chỉ xét các điểm $$, $$, $$, $$, và $$. Bây giờ, ta tính giá trị của hàm mục tiêu $$ tại các điểm này: - $$ - $$ - $$ - $$ - $$ Giá trị lớn nhất của hàm mục tiêu là 19 triệu đồng, đạt được khi $$ và $$. Vậy lãi suất cao nhất mà đơn vị thu được là 19 triệu đồng. Câu 4. Để giải bài toán này, chúng ta sẽ sử dụng công thức về số phần tử của hai tập hợp giao nhau. Gọi A là tập hợp các khách du lịch đến thăm động Thiên Cung. Gọi B là tập hợp các khách du lịch đến thăm đảo Titop. Theo đề bài, tổng số khách du lịch được phỏng vấn là 1410 khách, tức là: |A ∪ B| = 1410 Số khách du lịch đến thăm động Thiên Cung là 789 khách, tức là: |A| = 789 Số khách du lịch đến thăm đảo Titop là 690 khách, tức là: |B| = 690 Ta cần tìm số khách du lịch vừa đến thăm động Thiên Cung vừa đến thăm đảo Titop, tức là số phần tử của giao của hai tập hợp A và B, |A ∩ B|. Theo công thức về số phần tử của hai tập hợp giao nhau: |A ∪ B| = |A| + |B| - |A ∩ B| Thay các giá trị đã biết vào công thức: 1410 = 789 + 690 - |A ∩ B| Giải phương trình này để tìm |A ∩ B|: 1410 = 1479 - |A ∩ B| |A ∩ B| = 1479 - 1410 |A ∩ B| = 69 Vậy có 69 khách du lịch vừa đến thăm động Thiên Cung vừa đến thăm đảo Titop ở vịnh Hạ Long. Đáp số: 69 khách du lịch.