Giúp em với ạ

Câu 12. Để giải bài toán này, chúng ta cần xác định tọa độ của điểm B, sau đó tính khoảng cách giữa hai điểm A và B. Bước 1: Xác định tọa độ của điểm B. - Điểm B là hình chiếu của điểm A lên trục Ox, do đó tọa độ của B sẽ là (-5, 0, 0). Bước 2: Tính khoảng cách giữa hai điểm A và B. - Công thức tính khoảng cách giữa hai điểm \(A(x_1, y_1, z_1)\) và \(B(x_2, y_2, z_2)\) trong không gian là: \[ AB = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \] Áp dụng công thức trên vào tọa độ của điểm A(-5, 2, 3) và điểm B(-5, 0, 0): \[ AB = \sqrt{((-5) - (-5))^2 + (0 - 2)^2 + (0 - 3)^2} \] \[ AB = \sqrt{(0)^2 + (-2)^2 + (-3)^2} \] \[ AB = \sqrt{0 + 4 + 9} \] \[ AB = \sqrt{13} \] Vậy độ dài đoạn thẳng AB là \(\sqrt{13}\). Đáp án đúng là: B. \(\sqrt{13}\). Câu 1. Để giải quyết câu hỏi này, chúng ta sẽ kiểm tra từng phần của câu hỏi theo thứ tự. 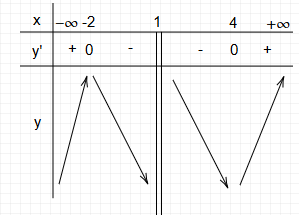a) Hàm số đồng biến trên khoảng (-∞; -2) Đầu tiên, chúng ta tính đạo hàm của hàm số: \[ y' = \left(\frac{x^2 + x + 7}{x - 1}\right)' = \frac{(2x + 1)(x - 1) - (x^2 + x + 7)}{(x - 1)^2} = \frac{x^2 - 2x - 8}{(x - 1)^2} \] Phương trình đạo hàm bằng 0: \[ x^2 - 2x - 8 = 0 \] \[ (x - 4)(x + 2) = 0 \] \[ x = 4 \text{ hoặc } x = -2 \] Từ đó, ta thấy rằng đạo hàm \( y' > 0 \) trên khoảng (-∞; -2). Do đó, hàm số đồng biến trên khoảng (-∞; -2). b) Đường tiệm cận xiên của đồ thị hàm số là đường thẳng y = x - 2 Ta thực hiện phép chia đa thức: \[ \frac{x^2 + x + 7}{x - 1} = x + 2 + \frac{9}{x - 1} \] Khi \( x \to \infty \) hoặc \( x \to -\infty \), ta có: \[ y \approx x + 2 \] Do đó, đường tiệm cận xiên của đồ thị hàm số là đường thẳng y = x + 2. c) Đồ thị hàm số cắt trục tung tại điểm A(0; -7) Thay x = 0 vào hàm số: \[ y = \frac{0^2 + 0 + 7}{0 - 1} = -7 \] Do đó, đồ thị hàm số cắt trục tung tại điểm A(0; -7). d) Đồ thị hàm số có hai điểm cực trị Từ phần a), ta đã tìm được đạo hàm: \[ y' = \frac{x^2 - 2x - 8}{(x - 1)^2} \] Đạo hàm bằng 0 tại x = 4 và x = -2. Ta kiểm tra dấu của đạo hàm ở các khoảng: - Trên khoảng (-∞; -2), \( y' > 0 \) - Trên khoảng (-2; 1), \( y' < 0 \) - Trên khoảng (1; 4), \( y' < 0 \) - Trên khoảng (4; ∞), \( y' > 0 \) Do đó, hàm số đạt cực đại tại x = -2 và cực tiểu tại x = 4. Vậy đồ thị hàm số có hai điểm cực trị. Kết luận: a) Đúng. b) Sai, đường tiệm cận xiên là y = x + 2. c) Đúng. d) Đúng. Đáp án: a, c, d. Câu 2. a) Ta có $f'(x) = 3x ^ 2 - 6x + 2$. Do đó $\int_{3}^{4}[f(x) + \frac{f'(x)}{f(x)}] dx = (\frac{x^4}{4} - x^3 + x^2 - x + ln|f(x)|) |_{3}^{4} = ln\frac{25}{3} + \frac{51}4$. Vậy mệnh đề đúng. b) Ta có $F'(x) = f(x) = x ^ 3 - 3x ^ 2 + 2x - 1$. Vậy mệnh đề đúng. c) Ta có $(\frac14x^4-x^3+x^2-x)' = x ^ 3 - 3x ^ 2 + 2x - 1 = f(x)$. Vậy mệnh đề đúng. d) Ta có $F(x) = \frac{x^4}{4} - x^3 + x^2 - x + C$. Mà $F(0) = 1$ nên $C = 1$. Vậy $F(x) = \frac{x^4}{4} - x^3 + x^2 - x + 1$. Suy ra $F(1) = \frac14 - 1 + 1 - 1 + 1 = \frac14$. Vậy mệnh đề sai. Câu 3. Để giải quyết các mệnh đề trên, chúng ta sẽ lần lượt kiểm tra từng mệnh đề dựa trên thông tin đã cho. a) Chi phí trung bình mỗi mét khối sản phẩm thấp nhất khi sản lượng nước tinh khiết trong ngày là $100~m^3$. Chi phí trung bình mỗi mét khối sản phẩm là: \[ \overline{c}(x) = \frac{C(x)}{x} \] Trước tiên, ta cần tính $C(x)$: \[ C(x) = 0,0003x^2 + 0,15x + 3 \] Do đó: \[ \overline{c}(x) = \frac{0,0003x^2 + 0,15x + 3}{x} = 0,0003x + 0,15 + \frac{3}{x} \] Để tìm giá trị nhỏ nhất của $\overline{c}(x)$, ta tính đạo hàm của $\overline{c}(x)$: \[ \overline{c}'(x) = 0,0003 - \frac{3}{x^2} \] Đặt $\overline{c}'(x) = 0$: \[ 0,0003 - \frac{3}{x^2} = 0 \] \[ \frac{3}{x^2} = 0,0003 \] \[ x^2 = \frac{3}{0,0003} = 10000 \] \[ x = 100 \] Vậy, chi phí trung bình mỗi mét khối sản phẩm thấp nhất khi sản lượng nước tinh khiết trong ngày là $100~m^3$. Mệnh đề này là đúng. b) $\overline{c}(x) = 0,0003x + 0,15 + \frac{3}{x}$. Ta đã tính $\overline{c}(x)$ ở trên: \[ \overline{c}(x) = 0,0003x + 0,15 + \frac{3}{x} \] Mệnh đề này là đúng. c) Chi phí sản xuất $100~m^3$ nước tinh khiết là 20 triệu đồng. Ta tính $C(100)$: \[ C(100) = 0,0003 \times 100^2 + 0,15 \times 100 + 3 \] \[ C(100) = 0,0003 \times 10000 + 15 + 3 \] \[ C(100) = 3 + 15 + 3 = 21 \text{ triệu đồng} \] Mệnh đề này là sai vì chi phí sản xuất $100~m^3$ nước tinh khiết là 21 triệu đồng, không phải 20 triệu đồng. d) $C(x) = 0,0003x^2 + 0,15x + 5$. Ta đã tính $C(x)$ ở trên: \[ C(x) = 0,0003x^2 + 0,15x + 3 \] Mệnh đề này là sai vì chi phí cố định là 3 triệu đồng, không phải 5 triệu đồng. Kết luận: - Mệnh đề a) là đúng. - Mệnh đề b) là đúng. - Mệnh đề c) là sai. - Mệnh đề d) là sai. Câu 4. a) Tọa độ hình chiếu của điểm B trên mặt phẳng Oxy là $H(2;1;0).$ b) Tọa độ của véc tơ là $\overrightarrow{AB}=(1;3;-2).$ c) $\overrightarrow x=2\overrightarrow{AB}-3\overrightarrow{BC}.$ Tọa độ của véc tơ $\overrightarrow x=(2;12;14)$ d) Tọa độ trọng tâm của tam giác ABC là $G(1;\frac23;0).$ Câu 1. Để xác định khoảng cách giữa hai chiếc khinh khí cầu, chúng ta sẽ sử dụng công thức tính khoảng cách giữa hai điểm trong không gian ba chiều. Đầu tiên, chúng ta xác định tọa độ của mỗi chiếc khinh khí cầu dựa trên thông tin đã cho. 1. Xác định tọa độ của chiếc khinh khí cầu thứ nhất: - Chiếc khinh khí cầu thứ nhất cách điểm xuất phát về phía Đông 100 km và về phía Nam 80 km, đồng thời cách mặt đất 1 km. - Tọa độ của chiếc khinh khí cầu thứ nhất là \( A(100, -80, 1) \). 2. Xác định tọa độ của chiếc khinh khí cầu thứ hai: - Chiếc khinh khí cầu thứ hai cách điểm xuất phát về phía Bắc 70 km và về phía Tây 60 km, đồng thời cách mặt đất 0,8 km. - Tọa độ của chiếc khinh khí cầu thứ hai là \( B(-60, 70, 0,8) \). 3. Áp dụng công thức tính khoảng cách giữa hai điểm trong không gian ba chiều: \[ d(A, B) = \sqrt{(x_2 - x_1)^2 + (y_2 - y_1)^2 + (z_2 - z_1)^2} \] Thay tọa độ của hai điểm vào công thức: \[ d(A, B) = \sqrt{((-60) - 100)^2 + (70 - (-80))^2 + (0,8 - 1)^2} \] \[ d(A, B) = \sqrt{(-160)^2 + (150)^2 + (-0,2)^2} \] \[ d(A, B) = \sqrt{25600 + 22500 + 0,04} \] \[ d(A, B) = \sqrt{48100,04} \] \[ d(A, B) \approx 219,32 \] Kết quả làm tròn đến hàng đơn vị: \[ d(A, B) \approx 219 \text{ km} \] Vậy khoảng cách giữa chiếc khinh khí cầu thứ nhất và chiếc khinh khí cầu thứ hai là 219 km. Câu 2. Để tìm điểm cực tiểu của đồ thị hàm số $y = x^3 + 3x^2 - 9x + 1$, ta thực hiện các bước sau: Bước 1: Tính đạo hàm của hàm số: \[ y' = \frac{d}{dx}(x^3 + 3x^2 - 9x + 1) = 3x^2 + 6x - 9 \] Bước 2: Tìm các điểm cực trị bằng cách giải phương trình đạo hàm bằng 0: \[ 3x^2 + 6x - 9 = 0 \] Chia cả hai vế cho 3: \[ x^2 + 2x - 3 = 0 \] Phương trình này có dạng bậc hai, ta giải bằng công thức: \[ x = \frac{-b \pm \sqrt{b^2 - 4ac}}{2a} \] Ở đây, \( a = 1 \), \( b = 2 \), \( c = -3 \): \[ x = \frac{-2 \pm \sqrt{2^2 - 4 \cdot 1 \cdot (-3)}}{2 \cdot 1} = \frac{-2 \pm \sqrt{4 + 12}}{2} = \frac{-2 \pm \sqrt{16}}{2} = \frac{-2 \pm 4}{2} \] Do đó: \[ x_1 = \frac{-2 + 4}{2} = 1 \] \[ x_2 = \frac{-2 - 4}{2} = -3 \] Bước 3: Xác định tính chất của các điểm cực trị bằng cách kiểm tra đạo hàm cấp hai: \[ y'' = \frac{d}{dx}(3x^2 + 6x - 9) = 6x + 6 \] Kiểm tra tại \( x = 1 \): \[ y''(1) = 6 \cdot 1 + 6 = 12 > 0 \] Vậy \( x = 1 \) là điểm cực tiểu. Kiểm tra tại \( x = -3 \): \[ y''(-3) = 6 \cdot (-3) + 6 = -18 + 6 = -12 < 0 \] Vậy \( x = -3 \) là điểm cực đại. Bước 4: Tìm tọa độ của điểm cực tiểu \( M(a; b) \): \[ a = 1 \] Thay \( x = 1 \) vào hàm số để tìm \( b \): \[ b = 1^3 + 3 \cdot 1^2 - 9 \cdot 1 + 1 = 1 + 3 - 9 + 1 = -4 \] Vậy điểm cực tiểu là \( M(1; -4) \). Bước 5: Tính \( a + b \): \[ a + b = 1 + (-4) = -3 \] Đáp số: \( a + b = -3 \) Câu 3. Để giải quyết bài toán này, chúng ta cần biết thêm thông tin về mối liên hệ giữa giá bán và lượng xoài bán được. Tuy nhiên, giả sử rằng lượng xoài bán được tăng lên theo tỷ lệ thuận với giảm giá bán. Chúng ta sẽ áp dụng phương pháp này để giải quyết bài toán. Giả sử giá bán giảm đi một phần trăm nào đó, lượng xoài bán được sẽ tăng lên tương ứng. Ta sẽ tính toán dựa trên giả thiết này. Bước 1: Xác định giá bán ban đầu và lượng xoài bán được ban đầu. - Giá bán ban đầu: 50000 đồng/kg - Lượng xoài bán được ban đầu: 25 kg Bước 2: Giả sử giá bán giảm đi một phần trăm nào đó, lượng xoài bán được sẽ tăng lên tương ứng. Ta sẽ tính toán dựa trên giả thiết này. Giả sử giá bán giảm đi 10%, tức là giá mới là: \[ 50000 - 50000 \times \frac{10}{100} = 50000 - 5000 = 45000 \text{ đồng/kg} \] Lượng xoài bán được sẽ tăng lên tương ứng. Nếu giá giảm 10%, lượng xoài bán được có thể tăng lên 10% (giả sử tỷ lệ thuận): \[ 25 + 25 \times \frac{10}{100} = 25 + 2.5 = 27.5 \text{ kg} \] Bước 3: Tính doanh thu trước và sau khi giảm giá. - Doanh thu ban đầu: \[ 50000 \times 25 = 1250000 \text{ đồng} \] - Doanh thu sau khi giảm giá: \[ 45000 \times 27.5 = 1237500 \text{ đồng} \] Bước 4: So sánh doanh thu trước và sau khi giảm giá. - Doanh thu ban đầu: 1250000 đồng - Doanh thu sau khi giảm giá: 1237500 đồng Như vậy, doanh thu sau khi giảm giá thấp hơn doanh thu ban đầu. Vì vậy, việc giảm giá không mang lại lợi ích về mặt doanh thu trong trường hợp này. Kết luận: Với giả thiết trên, việc giảm giá bán từ 50000 đồng/kg xuống 45000 đồng/kg làm tăng lượng xoài bán được từ 25 kg lên 27.5 kg, nhưng doanh thu lại giảm từ 1250000 đồng xuống 1237500 đồng. Do đó, việc giảm giá không mang lại lợi ích về mặt doanh thu trong trường hợp này.