Câu 1. Cho hình chóp S.ABC có đáy là tam giác đều cạnh a, SB 1 (ABC) và SB = 4a. Tính góc giữa đường thẳng SC và mặt phẳng (SAB)? Câu 2. Một người gửi tiết kiệm 100 triệu đồng vào ngân hàng theo thể th...

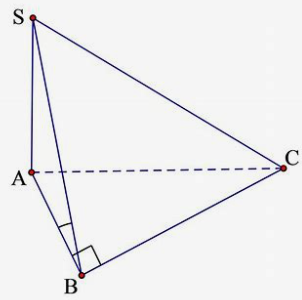
Câu 1. Để tính góc giữa đường thẳng SC và mặt phẳng (SAB), ta thực hiện các bước sau: 1. Xác định trực giao từ điểm C xuống mặt phẳng (SAB): - Vì SB vuông góc với đáy ABC, nên SB cũng vuông góc với mọi đường thẳng nằm trong mặt phằng (ABC). - Ta hạ đường cao CH từ C xuống SB, do SB vuông góc với đáy ABC, nên CH sẽ vuông góc với SB. - Mặt khác, vì SB nằm trong mặt phẳng (SAB), nên CH cũng vuông góc với mọi đường thẳng nằm trong mặt phẳng (SAB). 2. Tính góc giữa đường thẳng SC và mặt phẳng (SAB): - Góc giữa đường thẳng SC và mặt phẳng (SAB) chính là góc giữa SC và SH, tức là góc $$. 3. Tính độ dài các đoạn thẳng liên quan: - Vì SB vuông góc với đáy ABC, nên SB là đường cao của tam giác SBC. - Độ dài SB = 4a. - Độ dài BC = a (vì ABC là tam giác đều). - Độ dài CH = $$ (do CH là đường cao của tam giác đều ABC). 4. Áp dụng công thức tính góc: - Trong tam giác vuông SCH, ta có: $$ - Ta cần tính độ dài SC: $$ - Do đó: $$ 5. Kết luận: - Góc giữa đường thẳng SC và mặt phẳng (SAB) là góc $$, với $$. Đáp số: $$. Câu 2. Số tiền ban đầu người đó gửi tiết kiệm là 100 triệu đồng. Lãi suất 6 tháng là: $$ Sau mỗi 6 tháng, số tiền trong tài khoản sẽ tăng lên theo công thức lãi kép: $$ Trong đó: - $$ là số tiền cuối cùng. - $$ là số tiền ban đầu. - $$ là lãi suất %. - $$ là số kì hạn. Ta cần tìm số kì hạn $$ sao cho số tiền cuối cùng $$ ít nhất là 120 triệu đồng. Thay các giá trị vào công thức: $$ $$ $$ Áp dụng phương pháp lôgarit để giải phương trình mũ: $$ $$ $$ Tính giá trị của $$: $$ Vì số kì hạn phải là số nguyên, ta làm tròn lên đến 5 kì hạn. Mỗi kì hạn là 6 tháng, nên tổng thời gian là: $$ Vậy sau ít nhất 30 tháng, người đó sẽ nhận được ít nhất 120 triệu đồng. Câu 3. Để tìm góc giữa hai mặt phẳng (ABC) và (OBC), ta thực hiện các bước sau: 1. Xác định các vectơ pháp tuyến: - Mặt phẳng (OBC) có vectơ pháp tuyến $$ vì OA vuông góc với OB và OC. - Mặt phẳng (ABC) có vectơ pháp tuyến $$, ta cần tìm vectơ này. 2. Tìm vectơ pháp tuyến của mặt phẳng (ABC): - Ta có $$ - Ta có $$ - Vectơ pháp tuyến của mặt phẳng (ABC) là $$ 3. Tính các vectơ: - $$ - $$ - $$ - $$ - $$ 4. Tính tích vector $$: $$ $$ $$ Vậy $$. 5. Tính góc giữa hai vectơ pháp tuyến: - $$ - $$ Tích vô hướng: $$ Độ dài của các vectơ: $$ $$ Góc giữa hai vectơ: $$ Vậy $$. Do đó, góc giữa hai mặt phẳng (ABC) và (OBC) là 30 độ. Câu 4. Để tính góc giữa hai đường thẳng BK và SC trong hình chóp S.ABCD, ta thực hiện các bước sau: 1. Xác định các điểm và đường thẳng: - Đáy ABCD là hình vuông. - H là trung điểm của AB. - K là trung điểm của AD. - SH vuông góc với mặt phẳng (ABCD). 2. Tọa độ hóa các điểm: Giả sử cạnh hình vuông ABCD có độ dài là $$. Ta chọn hệ tọa độ sao cho: - A(0, 0, 0) - B(a, 0, 0) - D(0, a, 0) - C(a, a, 0) - H là trung điểm của AB nên H$$ - K là trung điểm của AD nên K$$ - S nằm trên đường thẳng vuông góc với (ABCD) tại H, ta giả sử S có tọa độ (0, 0, h). 3. Tìm vectơ của các đường thẳng: - Vectơ BK: $$ - Vectơ SC: $$ 4. Tính góc giữa hai vectơ: Góc giữa hai vectơ $$ và $$ được tính bằng công thức: $$ - Tích vô hướng $$: $$ - Độ dài của $$: $$ - Độ dài của $$: $$ - Vậy: $$ 5. Kết luận: Góc giữa hai đường thẳng BK và SC là: $$ Đáp số: Góc giữa hai đường thẳng BK và SC là $$. Câu 1. Giả sử sau n năm kể từ năm 2021, diện tích nuôi ngao bãi triều đạt trên 1400 ha. Diện tích nuôi ngao bãi triều vào năm 2021 là 840 ha. Mỗi năm diện tích nuôi ngao bãi triều tăng 6%, tức là mỗi năm diện tích nuôi ngao bãi triều sẽ gấp lên 1,06 lần. Sau n năm, diện tích nuôi ngao bãi triều sẽ là: $$ Ta cần tìm n sao cho: $$ Chia cả hai vế cho 840: $$ $$ $$ $$ Bây giờ ta sẽ thử các giá trị của n để tìm ra giá trị nhỏ nhất thỏa mãn điều kiện trên. - Với n = 10: $$ (không thỏa mãn vì 1,7908 < 1,6667) - Với n = 11: $$ (thỏa mãn vì 1,9005 > 1,6667) Vậy sau 11 năm kể từ năm 2021, tức là vào năm 2032, diện tích nuôi ngao bãi triều của tỉnh Thái Bình sẽ đạt trên 1400 ha. Đáp số: Năm 2032 Câu 2. Số tiền lãi sau 5 năm 2 tháng người đó nhận được là: $$ Số tiền cả gốc lẫn lãi sau 5 năm 2 tháng người đó nhận được là: $$ Đáp số: 26.620.000 đồng Câu 3. Để tìm tất cả các giá trị nguyên của tham số $$ sao cho phương trình $$ có nghiệm thuộc đoạn $$, chúng ta sẽ thực hiện các bước sau: 1. Xác định miền giá trị của $$ khi $$ thuộc đoạn $$: - Khi $$: $$ - Khi $$: $$ Do đó, khi $$ thay đổi từ 0 đến 2, giá trị của $$ thay đổi từ 8 xuống $$. 2. Xác định miền giá trị của $$: - Ta cần tìm các giá trị nguyên của $$ sao cho $$ nằm trong khoảng $$. 3. Kiểm tra các giá trị nguyên của $$: - Khi $$: $$ - Khi $$: $$ - Khi $$: $$ - Khi $$: $$ - Khi $$: $$ - Khi $$: $$ Các giá trị $$ đều nằm trong khoảng $$ khi $$ là các giá trị nguyên từ -2 đến 3. 4. Kết luận: Các giá trị nguyên của $$ sao cho phương trình $$ có nghiệm thuộc đoạn $$ là: $$ Đáp số: $$. Câu 4. Trước tiên, ta xác định các điểm và đường thẳng liên quan: - Hình chóp S.ABC có SA vuông góc với (ABC), SA = a. - Tam giác ABC vuông cân tại đỉnh A và BC = a√2. - M, N lần lượt là trung điểm của SB, SC. Ta cần tính cosin của góc tạo bởi hai mặt phẳng (AMN) và (ABC). Bước 1: Xác định các điểm và đường thẳng liên quan - Vì M và N là trung điểm của SB và SC nên MN song song với BC và MN = $$BC = $$. - Mặt phẳng (AMN) chứa đường thẳng AM và AN. Bước 2: Xác định góc giữa hai mặt phẳng - Góc giữa hai mặt phẳng (AMN) và (ABC) là góc giữa hai đường thẳng AM và AC (vì AC nằm trong mặt phẳng (ABC) và AM nằm trong mặt phẳng (AMN)). Bước 3: Tính độ dài các đoạn thẳng - Vì tam giác ABC vuông cân tại A, nên AB = AC = a. - Ta có SA = a và SA vuông góc với (ABC), do đó tam giác SAB và SAC đều là tam giác vuông cân tại A. - Do M là trung điểm của SB, nên AM = $$SA = $$. Bước 4: Tính cosin của góc AMN - Ta có AM = $$, AC = a và MN = $$. - Ta sử dụng công thức tính cosin trong tam giác AMN: $$ - Ta cần tính AN: $$ - Thay vào công thức: $$ $$ $$ $$ $$ Vậy cosin của góc tạo bởi hai mặt phẳng (AMN) và (ABC) là $$.