cho hình chóp s.abcd có sa vuông góc với mặt phẳng abcd,sa=3,abcd là hình vuông cạnh =1. tính khoảng cách giữa đường thẳng ac và sb..Giúp mình với!
 0
0
Làm sao để có câu trả lời hay nhất?
- Luôn có GIẢI THÍCH các bước giải
- Không copy câu trả lời của Timi
- Không sao chép trên mạng
- Không spam câu trả lời để nhận điểm
- Spam sẽ bị khóa tài khoản



05/04/2025
 0
0
05/04/2025
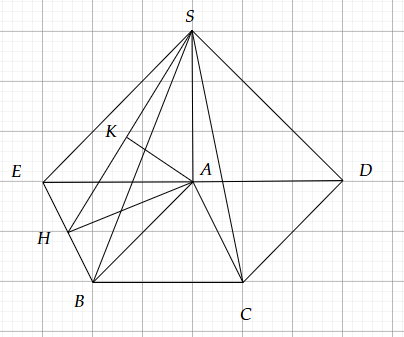
Dựng hình bình hành ACBE ⟹ AC//BE ⟹ AC // (SBE) nên
Trong (ABE) kẻ AK
Trong (SAK) kẻ AH
Vì ABCD là hình vuông nên AB
Xét tam giác vuông AEB, có:
Vì SA
 0
0
05/04/2025
Annh ThưChắc chắn rồi, hãy cùng giải bài toán này từng bước một:
1. Vẽ hình:
[Hình ảnh minh họa hình chóp S.ABCD, SA vuông góc (ABCD), ABCD là hình vuông cạnh 1, SA = 3]
2. Xác định đường vuông góc chung:
Gọi O là giao điểm của AC và BD.
Vì SA vuông góc (ABCD), nên SA vuông góc BD.
Vì ABCD là hình vuông, nên AC vuông góc BD.
Suy ra, BD vuông góc (SAC).
Trong mặt phẳng (SAC), kẻ OH vuông góc với SB (H thuộc SB).
Ta có: BD vuông góc (SAC), OH vuông góc SB, suy ra OH là đường vuông góc chung của AC và SB.
3. Tính độ dài OH:
Tam giác ABC vuông tại B, AB = BC = 1, suy ra AC = √2.
Tam giác SAC vuông tại A, SA = 3, AC = √2, suy ra SC = √(SA² + AC²) = √11.
Tam giác SBD vuông tại S, SB = √(SA² + AB²) = √10.
Tam giác SBO vuông tại S, SO = √(SA² + AO²) = √(9 + 1/2) = √(19/2).
Áp dụng hệ thức lượng trong tam giác vuông SBO:OH * SB = SO * AB
OH = (SO * AB) / SB = (√(19/2) * 1) / √10 = √(19/20) = √(190) / 20
4. Kết luận:
Khoảng cách giữa đường thẳng AC và SB là √(190) / 20.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
13 phút trước
15 phút trước
16 phút trước
Top thành viên trả lời



 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




