09/11/2023
Tìm đa thức f(x), biết rằng f(x) chia cho x-2 thì dư 3, f(x) chia cho x-3 thì dư 4 .Tìm số dư f(x) chia cho (x-2)(x-3) .
 0
0
-
Câu trả lời phải chính xác, đầy đủ dựa trên kiến thức xác thực:
- ✔ Đối với câu hỏi trắc nghiệm: Đưa đáp án lựa chọn + giải thích lý do chọn đáp án.
- ✔ Đối với câu hỏi tự luận: Đưa lời giải và đáp án cho câu hỏi.
- ✔ Đối với câu hỏi trả lời ngắn: Đưa ra đáp án + giải thích lý do.
- ✔ Chấp nhận sử dụng ảnh do thành viên viết tay, ảnh cần rõ nét, không bị mờ, vỡ ảnh.
- Sử dụng ngôn ngữ rõ ràng, dễ hiểu.
- Tránh đưa ra các ý kiến cá nhân mang tính chất chủ quan.
- Nếu sử dụng thông tin từ nguồn khác, phải trích dẫn nguồn đầy đủ và chính xác.
- Tuyệt đối không được sao chép các thông tin từ các trang khác, từ AI hoặc chatGPT.



09/11/2023
 0
0
09/11/2023
Vì
Khi đó
Theo bài cho ta có:
Vậy đa thức cần tìm là
Ta có:
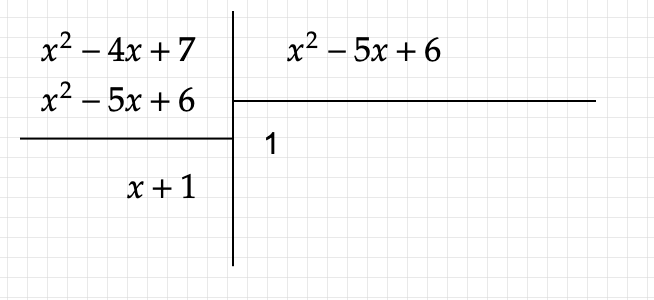
Số dư của
 0
0
09/11/2023
Để tìm số dư khi f(x) chia cho (x-2)(x-3), ta sử dụng định lý dư của phép chia đa thức. Theo định lý này, số dư khi f(x) chia cho một đa thức bậc nhất (ax + b) là f(-b/a).
Trong trường hợp này, f(x) chia cho x-2 thì dư 3 và f(x) chia cho x-3 thì dư 4. Áp dụng định lý dư, ta có:
f(2) = 3
f(3) = 4
Để tìm số dư f(x) chia cho (x-2)(x-3), ta sử dụng phương pháp phân tích thành thừa số. Ta giả sử f(x) có dạng:
f(x) = (x-2)(x-3)q(x) + r(x)
Trong đó q(x) là đa thức thương, r(x) là đa thức số dư cần tìm.
Vì f(x) chia cho (x-2)(x-3) nên r(x) là một đa thức bậc nhất hoặc không tồn tại.
Áp dụng điều kiện số dư, ta có:
r(2) = f(2) = 3
r(3) = f(3) = 4
Vì r(x) là một đa thức bậc nhất, ta có thể giả sử r(x) có dạng:
r(x) = ax + b
Áp dụng điều kiện số dư, ta có:
r(2) = 2a + b = 3
r(3) = 3a + b = 4
Giải hệ phương trình này, ta tìm được a = 1 và b = 1.
Vậy số dư f(x) chia cho (x-2)(x-3) là đa thức r(x) = x + 1.
 0
0
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
4 giờ trước
Top thành viên trả lời




 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




