BC là một dây cung của đường tròn $(\mathrm{O} ; \mathrm{R})(\mathrm{BC}
eq 2 \mathrm{R})$. Điểm A di động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC . Các đường cao $\mathrm{AD}, \mathrm{BE}, \mathrm{CF}$ của tam giác ABC đồng quy tại H .
1. Chứng minh tam giác AEF đồng dạng với tam giác ABC .
2. Gọi $\mathrm{A}^{\prime}$ là trung điểm của BC, Chứng minh $\mathrm{AH}=2 \mathrm{OA}^{\prime}$.
3. Gọi $\mathrm{A}_1$ là trung điểm của EF , Chứng minh $\mathrm{R} \cdot \mathrm{AA}_1=\mathrm{AA}^{\prime} \cdot \mathrm{OA}^{\prime}$.
4. Chứng minh $\mathrm{R}(\mathrm{EF}+\mathrm{FD}+\mathrm{DE})=2 \mathrm{~S}_{\mathrm{ABC}}$ suy ra vị trí của A để tổng $\mathrm{EF}+\mathrm{FD}+\mathrm{DE}$ đạt giá trị lớn nhất.

Question

BC là một dây cung của đường tròn $(\mathrm{O} ; \mathrm{R})(\mathrm{BC} 
eq 2 \mathrm{R})$. Điểm A di động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC . Các đường cao $\mathrm{AD}, \mathrm{BE}, \mathrm{CF}$ của tam giác ABC đồng quy tại H .
1. Chứng minh tam giác AEF đồng dạng với tam giác ABC .
2. Gọi $\mathrm{A}^{\prime}$ là trung điểm của BC, Chứng minh $\mathrm{AH}=2 \mathrm{OA}^{\prime}$.
3. Gọi $\mathrm{A}_1$ là trung điểm của EF , Chứng minh $\mathrm{R} \cdot \mathrm{AA}_1=\mathrm{AA}^{\prime} \cdot \mathrm{OA}^{\prime}$.
4. Chứng minh $\mathrm{R}(\mathrm{EF}+\mathrm{FD}+\mathrm{DE})=2 \mathrm{~S}_{\mathrm{ABC}}$ suy ra vị trí của A để tổng $\mathrm{EF}+\mathrm{FD}+\mathrm{DE}$ đạt giá trị lớn nhất.

Accepted Answer

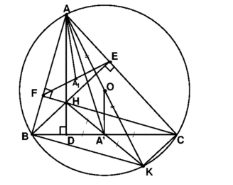
1. Tứ giác BFEC nội tiếp $=>\angle \mathrm{AEF}=\angle \mathrm{ACB}$ (cùng bù $\angle \mathrm{BFE}$ ) $\angle \mathrm{AEF}=\angle \mathrm{ABC}$ (cùng bù $\angle \mathrm{CEF}$ ) $=> riangle \mathrm{AEF} \sim riangle \mathrm{ABC}$.
2. Vẽ đường kính $\mathrm{AK}=>\mathrm{KB} / / \mathrm{CH}$ ( cùng vuông góc AB ); $\mathrm{KC} / / \mathrm{BH}$ (cùng vuông góc AC$)=>\mathrm{BHKC}$ là hình bình hành $=>\mathrm{A}^{\prime}$ là trung điểm của HK
$\Rightarrow \mathrm{OK}$ là đường trung bình của $ riangle \mathrm{AHK} \Rightarrow \mathrm{AH}=2 \mathrm{OA}^{\prime}$
3. Áp dụng tính chất : nếu hai tam giảc đồng dạng thi ti số giũ̃a hia trung tuyến, ti số giũra hai bản kinh các đường trờn ngoại tiếp bằng ti số đồng dạng. ta có :
$\Delta \mathrm{AEF} \sim \Delta \mathrm{ABC} \Rightarrow \frac{R}{R^{\prime}}=\frac{A A^{\prime}}{A A_1}(1)$ trong đó R là bán kính đường tròn ngoại tiếp $\Delta \mathrm{ABC} ; \mathrm{R}^{\prime}$ là bán kính đường tròn ngoại tiếp $ riangle \mathrm{AEF} ; \mathrm{AA}^{\prime}$ là trung tuyến của $ riangle \mathrm{ABC} ; \mathrm{AA}_1$ là trung tuyến của $ riangle \mathrm{AEF}$.
Tứ giác AEHF nội tiếp đường tròn đường kính AH nên đây cũng là đường tròn ngoại tiếp $ riangle \mathrm{AEF}$
Từ (1) $\Rightarrow>\mathrm{R} \cdot \mathrm{AA}_1=\mathrm{AA}^{\prime} \cdot \mathrm{R}^{\prime}=\mathrm{AA}^{\prime} \frac{A H}{2}=\mathrm{AA}^{\prime} \cdot \frac{2 A^{\prime} O}{2}$
Vậy $\quad \mathrm{R} \cdot \mathrm{AA}_1=\mathrm{AA}^{\prime} \cdot \mathrm{A}^{\prime} \mathrm{O}$
4. Gọi $\mathrm{B}^{\prime}, \mathrm{C}^{\prime}$ lần lượt là trung điểm của $\mathrm{AC}, \mathrm{AB}$, ta có $\mathrm{OB}^{\prime} \perp \mathrm{AC} ; \mathrm{OC} ' \perp \mathrm{AB}$ (bán kính đi qua trung điểm của một dây không qua tâm) $\Rightarrow \mathrm{OA}^{\prime}, \mathrm{OB}^{\prime}, \mathrm{OC}^{\prime}$ lần lượt là các đường cao của các tam giác $\mathrm{OBC}, \mathrm{OCA}$, OAB.

$$
\begin{aligned}
& \mathrm{S}_{\mathrm{ABC}}=\mathrm{S}_{\mathrm{OBC}}+\mathrm{S}_{\mathrm{OCA}}+\mathrm{S}_{\mathrm{OAB}}=\frac{1}{2}\left(\mathrm{OA}^{\prime} \cdot \mathrm{BC}^{\prime}+\mathrm{OB}^{\prime} \cdot \mathrm{AC}+\mathrm{OC}^{\prime} \cdot \mathrm{AB} ight) \
& 2 \mathrm{~S}_{\mathrm{ABC}}=\mathrm{OA}^{\prime} \cdot \mathrm{BC}+\mathrm{OB}^{\prime} \cdot \mathrm{AC}^{\prime}+\mathrm{OC}^{\prime} \cdot \mathrm{AB}
\end{aligned}
$$

Theo $(2) \Rightarrow \mathrm{OA}^{\prime}=\mathrm{R} \cdot \frac{A A_1}{A A^{\prime}}$ mà $\frac{A A_1}{A A^{\prime}}$ là tỉ số giữa 2 trung tuyến của hai tam giác đồng dạng AEF và ABC nên $\frac{A A_1}{A A^{\prime}}=\frac{E F}{B C}$. Tương tự ta có : $\mathrm{OB}^{\prime}=\mathrm{R} \cdot \frac{F D}{A C} ; \mathrm{OC}^{\prime}=\mathrm{R} \cdot \frac{E D}{A B}$ Thay vào (3) ta được $2 \mathrm{~S}_{\mathrm{ABC}}=\mathrm{R}\left(\frac{E F}{B C} \cdot B C+\frac{F D}{A C} \cdot A C+\frac{E D}{A B} \cdot A B ight) \Leftrightarrow 2 \mathrm{~S}_{\mathrm{ABC}}=\mathrm{R}(\mathrm{EF}+\mathrm{FD}+\mathrm{DE})$
* $\mathrm{R}(\mathrm{EF}+\mathrm{FD}+\mathrm{DE})=2 \mathrm{~S}_{\mathrm{ABC}}$ mà R không đổi nên $(\mathrm{EF}+\mathrm{FD}+\mathrm{DE})$ đạt gí trị lớn nhất khi $\mathrm{S}_{\mathrm{ABC}}$.

Ta có $\mathrm{S}_{\mathrm{ABC}}=\frac{1}{2} \mathrm{AD} \cdot \mathrm{BC}$ do BC không đồi nên $\mathrm{S}_{\mathrm{ABC}}$ lớn nhất khi AD lớn nhất, mà AD lớn nhất khi A là điểm chính giỡa của cung lớn BC .

BC là một dây cung của đường tròn . Điểm A di động trên cung lớn BC sao cho O luôn nằm trong tam giác ABC . Các đường cao...