ADS
Tài khoản ẩn danh
06/04/2025
giúp em với ạ

ADS
 0
0
Trả lời câu hỏi của Tài khoản ẩn danh
Làm sao để có câu trả lời hay nhất?
- Luôn có GIẢI THÍCH các bước giải
- Không copy câu trả lời của Timi
- Không sao chép trên mạng
- Không spam câu trả lời để nhận điểm
- Spam sẽ bị khóa tài khoản
ADS
CÂU TRẢ LỜI



Timi
06/04/2025
Trợ lý học tập AI - Câu trả lời này chỉ mang tính tham khảo
Câu 7:
Phương trình bậc hai một ẩn là phương trình có dạng
Hãy giúp mọi người biết câu trả lời này thế nào?
5.0/5 (1 đánh giá)
 0
0
0 bình luận
Bình luận
P_cutii
06/04/2025
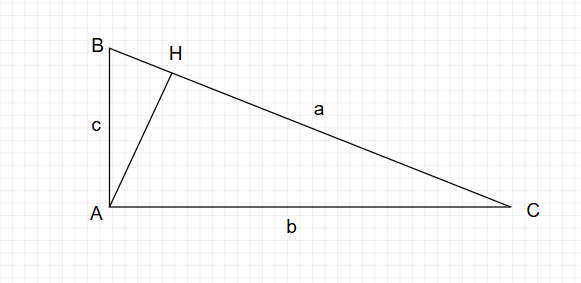
Câu 8 :
Suy ra
Suy ra
Chọn C
Câu 9 :
Chọn D
Câu 10 : B
Hãy giúp mọi người biết câu trả lời này thế nào?
0/5 (0 đánh giá)
 0
0
0 bình luận
Bình luận
ADS
Nếu bạn muốn hỏi bài tập
Các câu hỏi của bạn luôn được giải đáp dưới 10 phút
CÂU HỎI LIÊN QUAN
Quyền Nguyễn
1 giờ trước
Top thành viên trả lời
Chọn thời gian
Sabo(サボ) 17.000 Điểm
𝑩𝒆́ 𝑴𝒖̛𝒂 13.320 Điểm
Mua hàng shopee 13.260 Điểm
🔥8A_k11🔥 12.440 Điểm
Đóm 9.950 Điểm
FQA.vn Nền tảng kết nối cộng đồng hỗ trợ giải bài tập học sinh trong khối K12. Sản phẩm được phát triển bởi CÔNG TY TNHH CÔNG NGHỆ GIA ĐÌNH (FTECH CO., LTD)
Điện thoại: 1900636019
Email: info@fqa.vn
 Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Ô Chợ Dừa, Quận Đống Đa, Thành phố Hà Nội, Việt Nam.
Địa chỉ: Số 21 Ngõ Giếng, Phố Đông Các, Phường Ô Chợ Dừa, Quận Đống Đa, Thành phố Hà Nội, Việt Nam.
Người chịu trách nhiệm quản lý nội dung: Nguyễn Tuấn Quang
Giấy phép thiết lập MXH số 07/GP-BTTTT do Bộ Thông tin và Truyền thông cấp ngày 05/01/2024
Copyright © 2023 fqa.vn All Rights Reserved



 Toán Học
Toán Học
 Vật Lý
Vật Lý
 Hóa Học
Hóa Học
 Tiếng Anh
Tiếng Anh
 Ngữ Văn
Ngữ Văn
 Sinh Học
Sinh Học
 Địa Lý
Địa Lý
 GDCD
GDCD
 GDĐP
GDĐP
 Tin Học
Tin Học
 Công Nghệ
Công Nghệ
 Nhạc Họa
Nhạc Họa
 KHTN
KHTN
 Sử & Địa
Sử & Địa
 Khác
Khác




