Tổng hợp lý thuyết về phương trình mặt cầu lớp 12 và dạng bài tập

Phương trình mặt cầu được viết như thế nào? Mỗi dạng bài khác nhau sẽ có phương pháp giải riêng biệt để tìm ra phương trình mặt cầu chuẩn xác. Đây là một chuyên đề khó trong toán 12 và không phải học sinh nào cũng có thể học tốt và giải đúng. Hiểu được điều này, Admin sẽ cung cấp kiến thức lý thuyết phương trình mặt cầu, kèm thêm các dạng bài tập và cách giải chi tiết để các em tham khảo.

Ôn lại định nghĩa về mặt cầu

Muốn nắm vững kiến thức về phương trình mặt cầu lớp 12, đầu tiên các em cần có nền tảng về mặt cầu. Cùng Admin ôn lại một chút định nghĩa về mặt cầu như sau:

Mặt cầu là tập hơn tất cả các điểm cách đều một khoảng không đổi với một điểm cho trước. Khoảng cách cố định không đổi đó chính là bán kính của mặt cầu và tâm mặt cầu là điểm đã cho trước. Ngoài ra, mặt cầu còn được định nghĩa theo hướng mặt tròn xoay trong không gian. Khi đó, mặt cầu chính là mặt tròn xoay quanh một đường trong xung quanh một đường kính.

Tổng hợp lý thuyết phương trình mặt cầu lớp 12

Để có thể giải các dạng bài tập về phương trình đường cao trong chương trình toán lớp 12. Các em cần nắm trọn các kiến thức lý thuyết trọng tâm như sau:

Tổng hợp lý thuyết phương trình mặt cầu lớp 12

Phương trình mặt cầu trong không gian có mấy dạng?

Phương trình mặt cầu chia thành dạng tổng quát và dạng chính tắc. Cụ thể như sau:

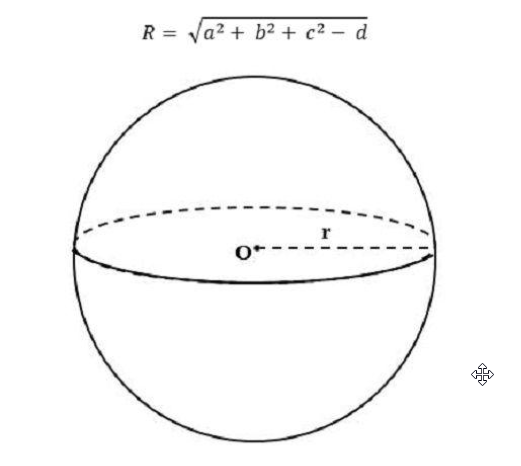
Phương trình mặt cầu trong không gian có mấy dạng?

Phương trình mặt cầu dạng tổng quát nhất

Cho một không gian có trục tọa độ Oxyz có mặt cầu S thỏa mãn điều kiện:

a² + b² + c² - d > 0

$\Rightarrow$ Phương trình mặt cầu (S) có bản như sau:

x² + y² + z² - 2ax - 2by - 2cz + d > 0

$\Rightarrow$ Công thức tính bán kính của mặt cầu (S) như sau:

$R=\sqrt{a^2+b^2+c^2-d}$

Phương trình mặt cầu chính tắc

Trong trường hợp các em biết bán kính R và tâm I (a; b; c) thì phương trình mặt cầu (S) chính tắc trong không gian Oxyz được viết như sau:

(x - a)² + (y - b)² + (z - c)² = R²

Công thức phương trình mặt cầu

Muốn viết phương trình mặt cầu, các em có thể viết theo cách đơn giản và dễ hiểu như sau:

Công thức phương trình mặt cầu và mặt phẳng

Cho một mặt cầu (S) có phương trình là: (x - a)² + (y - b)² + (z - c)² = R với tâm I (a ; b; c) và R là bán kính của mặt cầu (S). 

Khi đó ta viết phương trình mặt cầu tâm I (a; b; c) là: x² + y² + z² - 2ax -2by -2cz + d = 0

Công thức tính bán kính R của mặt cầu (S) là: $R=\sqrt{a^2+b^2+c^2-d}$

$\Rightarrow$ Công thức tính khoảng cách từ tâm I mặt cầu đến mặt phẳng để xét vị trí tương đối giữa mặt cầu (S) và mặt phẳng như sau:

$d(I,(P))=\frac{|A \cdot a+B \cdot b+C \cdot c+D|}{\sqrt{a^2+b^2+c^2}}$

Công thức phương trình mặt cầu tại vị trí tiếp xúc với đường thẳng

Khi một đường thẳng tiếp xúc với mặt cầu d(I, (P)) và mặt cầu (P), đồng thời nó cũng là tiếp diện của mặt cầu thì tọa độ hình chiếu của mặt cầu và mặt phẳng là điểm tiếp xúc của mặt cầu và mặt phẳng tại H, được ký hiệu là vecto IH (vecto pháp tuyến của mặt phẳng (P).

Các dạng bài tập phương trình mặt cầu thường gặp

Để giúp các có thể giải bài tập một cách dễ dàng và nhanh chóng nhất, giảm tỷ lệ giải sai và đạt điểm cao. Admin sẽ chia sẻ các dạng bài về phương trình mặt cầu thường gặp kèm cách giải và ví dụ chi tiết để các em tham khảo.

Dạng 1: Viết phương trình mặt cầu tâm I và bán kính

Đối với dạng bài viết phương trình mặt cầu khi đã biết tâm và bán kính, các em sẽ tiến hành giải theo 1 trong 2 phương pháp sau:

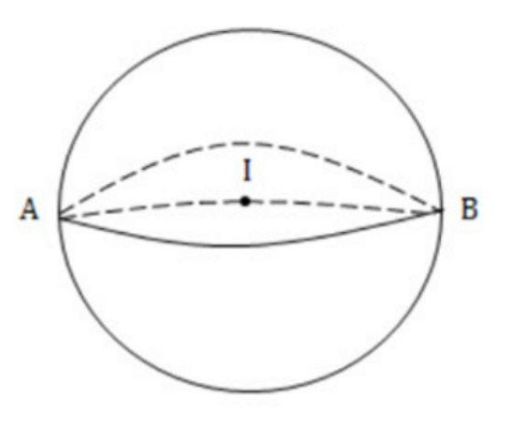
Dạng 1: Viết phương trình mặt cầu tâm I và bán kính

• Phương pháp 1: Giải theo cách viết phương trình mặt cầu dạng chính tắc. Các bước giải chi tiết như sau:
• Bước 1: Đầu tiên các em cần xác định tâm I (a; b; c) của mặt cầu (S)
• Bước 2: Tiến hành tìm bán kính R của mặt cầu (S)
• Bước 3: Viết phương trình mặt cầu (S) với tâm I (a; b; c) và bán kính R có dạng tổng quát như sau: (x - a)² + (y - b)² + (z - c)² = R²
• Phương pháp 2: Giải theo cách viết phương trình mặt cầu ở dạng tổng quát nhất. Các bước giải chi tiết như sau:
• Bước 1: Viết phương trình dạng tổng quát là: x² + y² + z² - 2ax - 2by - 2cz + d = 0
• Bước 2: Thêm điều kiện a² + b² + c² > 0 để phương trình mặt cầu (S) hoàn toàn xác định.

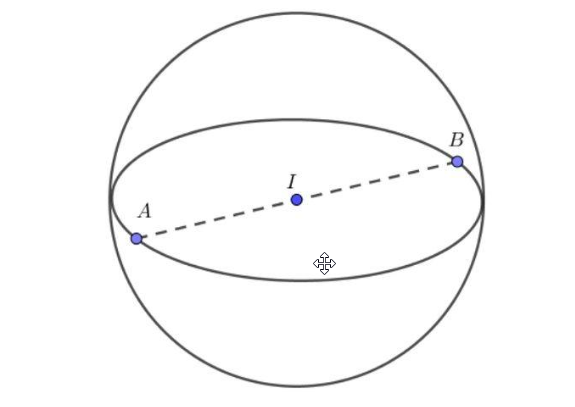
Ví dụ: Cho một đường kính AB có A (2; 1; 3) và B (0; -3; 1). Hãy tìm và viết công thức phương trình mặt cầu.

Hình ảnh minh họa cho ví dụ

Giải: 

Theo đề bài đường kính AB có A (2; 1; 3) và B (0; -3; 1)

$\Rightarrow$ Tâm I của mặt cầu là trung điểm của AB với tọa độ I (1; -1; 2)

Bán kính $R=\frac{1}{2} \cdot A B=\frac{1}{2} \cdot \sqrt{(0-2)^2+(-3-1)^2+(1-3)^2}=\sqrt{6}$

$\Rightarrow$ Phương trình mặt cầu có dạng:

(x - 1)² + (y + 1)² + (z - 2)² = 6

Dạng 2: Viết phương trình mặt cầu khi biết tâm và 1 điểm

Đối với dạng bài tập này, thông qua cách tích độ dài vecto từ tâm đến điểm mà mặt cầu đi qua, các em có thể tính được bán kính một cách cực dễ. Sau đó các em sẽ áp dụng phương pháp giải giống như ở dạng 1. Để hiểu rõ hơn, các em cùng đi vào ví dụ cụ thể dưới đây.

Dạng 2: Viết phương trình mặt cầu khi biết tâm và 1 điểm

Ví dụ: Cho một phương trình mặt cầu (S), có tâm I (1; 2; -3) đi qua điểm A (1; 0; 4). Hãy viết phương trình mặt cầu (S)?

Giải:

Theo đề bài ta có: $\overrightarrow{I A}=(0 ;-2 ; 7)$

$I A=|\overrightarrow{I A}|=\sqrt{53}$

Viết phương trình mặt cầu (S) có tâm I (1; 2; -3) và bán kính $I A=R=\sqrt{53}$ có dạng như sau:

(x - 1)² + (y - 2)² + (z + 3)² = 53

Dạng 3: Tìm dạng tổng quát của phương trình mặt cầu ngoại tiếp tứ diện

Đối với dạng bài này, cách giải các em sẽ áp dụng theo các bước chi tiết như sau:

Dạng 3: Tìm dạng tổng quát của phương trình mặt cầu ngoại tiếp tứ diện

• Bước 1: Đầu tiên các em cần gọi I(x; y; z) là tâm của mặt cầu (S)
• Bước 2: Thực hiện lập phương trình mặt cầu theo đề bài khi nó là ngoại tiếp tứ diện ABCD. Từ đó có có IA = IB = IC = ID.

$\Rightarrow$ IA² = IB² = IC² = ID²

$\Rightarrow$ a₁.x + b₁.y + c₁.z = d₁ và a₂.x + b₂.y + c₂.z = d₂ và a₃.x + b₃.y + c₃.z = d₃

• Bước 3: Các em đưa ra kết luận về tọa độ của tâm I, từ đó có thể suy ra được độ dài của bán kinh để viết phương trình mặt cầu (S) dạng cơ bản.

Ví dụ: Viết phương trình mặt cầu ngoại tiếp tứ diện ABCD khi biết tọa độ của 4 điểm là: 

• A (6; -2; 3)
• B (0; 1; 6)
• C (2; 0; -1)
• D (4; 1; 0)

Giải:

Gọi I (x; y; z) là tâm của mặt cầu ngoại tiếp tứ diện ABCD

$\begin{aligned} & \Rightarrow I A=I B=I C=I D \\ & \Rightarrow I A^2=I B^2=I C^2=I D^2 \\ & \Rightarrow(x-6)^2+(y+2)^2+(z-3)^2=x^2+(y-1)^2+(z-6)^2\end{aligned}$

và (x - 6)² + (y + 2)² + (z - 3)² = (x - 2)² + y² + (z + 1)²

và (x - 6)² + (y + 2)² + (z - 3)² = (x - 4)² + (y - 1)² + z²

$\Rightarrow$ 2x - y - z = 2 và 2x - y + 2z = 11 và 2x - 3y + 3z = 16 

$\Rightarrow$ x = 2, y = -1 và z = 3

$\Rightarrow$ IA² = R² = 17

$\Rightarrow$ Phương trình mặt cầu (S) ngoại tiếp tứ diện ABCD có dạng là:

(x - 2)² + (x + 1)² + (z - 3)² = 17

Dạng 4: Viết phương trình mặt cầu từ 4 điểm OABC

Đối với dạng bài này, các em còn có thể gặp một dạng biến thể khác khi ra đề bài là: Viết phương trình mặt cầu (S) đi qua 3 điểm A, B và C có tâm nằm trên mặt phẳng (P) cho trường. Các em sẽ thực hiện giải dạng bài tập này theo các bước chi tiết như sau:

Dạng 4: Viết phương trình mặt cầu từ 4 điểm OABC

• Bước 1: Đầu tiên các em cần gọi tầm mặt cầu (S) là I (a; b; c) nằm trên mặt phẳng (P)
• Bước 2: Các em lập hệ phương trình với IA = IB và IA = IC (I ∊ (P))
• Bước 3: Tiến hành giải hệ phương trình mà các em đã lập ở bước trên. Sau đó thay kết quả tìm được vào phương trình để tìm ra bán kính.
• Bước 4: Cuối cùng viết phương trình mặt cầu (S) hoàn chỉnh.

Ví dụ: Cho 3 điểm A (1; 0; 1) B (1; 0; 0) và C (1; 1; 1). Hãy viết phương trình mặt cầu (S) có tâm nằm trên mặt phẳng (P): x + y + z - 2 = 0

Giải:

Gọi phương trình mặt cầu (S) tổng quát có dạng là:

x² + y² + z² - 2ax - 2by - 2cz + d = 0 (a² + b² + c² > d₁)

Mặt cầu (S) có tâm I (-a; -b; -c)

Khi đó ta lập được hệ phương trình như sau:

4 + 1 + 4a + 2c + d = 0 và 1 + 2c + d = 0 và 3 + 3a + 2b + 2c + d = 0 và - a - b - c - 2 = 0

$\Rightarrow$ 4a + 2c + d = -5 và 2c + d = -1 và 2a + 2b + 2c + d = -3 và a + b + bc = -2

$\Rightarrow$ a = -1; b = 0, c = -1 và d = 1

Thay vào phương trình mặt cầu (S) dạng tổng quát ở đầu, ta được phương trình mặt cầu hoàn chỉnh là:

x² + y² + z² + 1 = 0

Dạng 5: Viết phương trình mặt cầu đi qua 4 điểm

Để giải được bài tập dạng viết phương trình mặt cầu đi qua 4 điểm, các em sẽ thực hiện việc lập hệ phương trình 4 ẩn giống dạng 4 được chia sẻ ở trên. Sau khi giải hệ phương trình và tìm ra được đáp án, các em thay vào phương trình mặt cầu dạng tổng quát là ra kết quả.

Ví dụ: Cho 4 điểm A (2; 0; 0), B (1; 3; 0), C (-1; 0; 3) và D (1; 2; 3). Tất cả 4 điểm này đều đi qua mặt cầu (S). Hỏi bán kính R của mặt cầu (S) là bao nhiêu?

Giải:

Gọi I là tâm của mặt cầu (S) với tọa độ (a; b; c) đi qua 4 điểm A (2; 0; 0), B (1; 3; 0), C (-1; 0; 3) và D (1; 2; 3).

$\Rightarrow$ Hệ phương trình như sau:

(a - 2)² + b² + c² = (a - 1)² + (b - 3)² + c² và (a - 2)² + b² + c² = (a + 1)² + b² + (c - 3)²

và (a + 1)² + b² + (c - 3)² = (a - 1)² + (b - 2)² + (c - 3)²

$\Rightarrow$ -4a + 4 = -2a + 1 - 6b + 9 và -4a + 4 = 2a + 1 - 6c + 9 và 2a + 1 = -2a + 1 - 4b + 4

$\Rightarrow$ a = 0; b ; 1 và c = 1

$\Rightarrow$ Tâm I (0; 1; 1)

$\Rightarrow I A=R=\sqrt{\left(2^2+1^2+1^2\right)}=\sqrt{6}$

Dạng 6: Viết phương trình mặt cầu với 2 điểm cho trước

Phương pháp giải đối với dạng bài tập này sẽ được áp dụng tương tự cách viết phương trình mặt cầu (S) có đường kính AB cho trước. Chi tiết các bước giải cụ thể như sau:

• Bước 1: Đầu tiên các em cần tìm trung điểm của AB, từ đó có thể suy ra được I chính là trung điểm của AB và chính là tâm của mặt cầu.
• Bước 2: Các em cần tính bánh kính R = IA
• Bước 3: Đưa phương trình về dạng bài tập 1 cơ bản để giải một cách dễ dàng và đơn giản nhất.

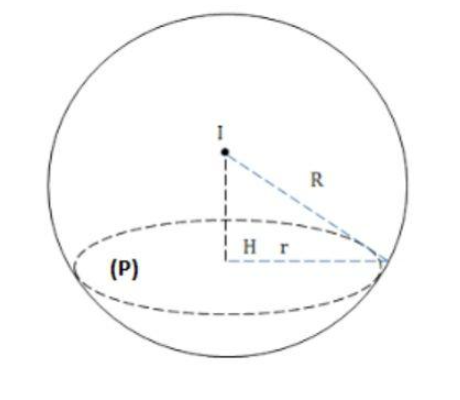
Dạng 6: Viết phương trình mặt cầu với 2 điểm cho trước

Ví dụ: Viết một phương trình mặt cầu (S) khi biết đường kính AB của mặt cầu có 2 điểm A (-2; 1; 0) và B (2; 3; -2).

Giải:

Gọi I là trung điểm của bán kính AB

$\Rightarrow$ Tọa độ điểm I (x; y; z) là: $x=\frac{-2+2}{2}=0 ; y=\frac{1+3}{2}=2 ; z=\frac{0-2}{2}=-1$

$\Rightarrow$ I (0; 2; -1)

Độ dài của bán kính $R=I A=\sqrt{(-2-0)^2+(1+2)^2+(0+1)^2}=\sqrt{6}$

$\Rightarrow$ Phương trình mặt cầu (S) có dạng là:

(x - 0)² + (y - 2)² + (z + 1)² = 6 ⇔ x² + (y - 2)² + (z + 1)² = 6

Dạng 7: Tìm điều kiện và giá trị m để phương trình là phương trình mặt cầu

So với 6 dạng đã được Admin chia sẻ ở trên, thì dạng thứ 7 này là dạng bài tập nâng cao của phương trình mặt cầu (S). Muốn giải được bài tập này, các em cần áp dụng tính chất nhận biết và điều kiện của phương trình mặt cầu như a² + b² + c² - d > 0 để giải và tìm ra đáp án chính xác.

Ví dụ: Cho một hệ tọa độ Oxyz trong không gian, tìm m để phương trình:

x² + y² + z² + 2x - 4y + 4z + m = 0 là một phương trình mặt cầu (S).

Giải:

Theo đề bài ta có: a = -1; b = 2; c = -2; d = m

Phương trình x² + y² + z² + 2x - 4y + 4z + m = 0 là một phương trình mặt cầu (S) khi và chỉ khi: (-1)² + 2² + (-2)² - m > 0 $\Rightarrow$  9 - m > 0 $\Rightarrow$  m < 9

Như vậy, toàn bộ kiến thức trong bài viết trên được Admin chia sẻ không chỉ giúp các em nắm trọn lý thuyết về phương trình mặt cầu. Mà còn bỏ túi được các dạng bài cùng phương pháp giải bài tập. Hãy lưu bài viết này lại để đọc nhiều lần và áp dụng cho bản thân vào việc giải toán về phương trình mặt cầu nhé! Chúc các em thành công và luôn đạt điểm cao với toán 12.