Để giúp các em luyện tập kỹ hơn về phần kiến thức hình nón, cũng như cách tính thể tích, Admin đã tổng hợp lại 15 câu trắc nghiệm liên quan. Các em hãy vận dụng những kiến thức đã học để giải những đề bài dưới đây nhé!
Xem chi tiết công thức tính thể tích khối nón tại: Không bao giờ được phép quên công thức tính thể tích khối nón!
Bổ sung thêm công thức tính diện tích đáy hình nón: Công thức tính diện tích xung quanh hình nón kèm bài tập
ĐỀ BÀI
Câu 1. Hình nón có đường sinh $l=2a$ và hợp với đáy góc $\text{a}=60{}^\circ $. Diện tích toàn phần của hình nón bằng:
A. $4 \pi a^2$
B. $3 \pi a^2$
C. $2 \pi a^2$
D. $\pi a^2$
Câu 2. Cho hình nón đỉnh $S$ có bán kính đáy $r=a \sqrt{2}$, góc ở đỉnh bằng $60{}^\circ $. Diện tích xung quanh của hình nón bằng:
A. $4 \pi a^2$
B. $3 \pi a^2$
C. $2 \pi a^2$
D. $\pi a$
Câu 3. (ĐỀ MINH HỌA QUÓC GIA NĂM 2017) Trong không gian, cho tam giác ABC vuông tại $A,\,\,\,AB=a,AC=a\sqrt{{}}3$. Độ dài đường sinh l của hình nón nhận được khi quay tam giác A B C xung quanh trục AB bằng:
A. $I=a$
B. $I=a \sqrt{ } 2$
C. $I=a \sqrt{3}$
D. $I=2 a$
Câu 4. Thiết diện qua trục hình nón là một tam giác vuông cân có cạnh góc vuông bằng a. Diện tích toàn phần của hình nón có giá trị là:
A. $\frac{(1+\sqrt{2})\pi {{a}^{2}}}{2}$
B. $\frac{\sqrt{2}\pi {{a}^{2}}}{2}$ .
C. $\frac{(1+\sqrt{2})\pi {{a}^{2}}}{2}$ .
D. $\frac{\sqrt{2}\pi {{a}^{2}}}{2}$ .
Câu 5. Cạnh bên của một hình nón bằng 2a. Thiết diện qua trục của nó là một tam giác cân có góc ở đỉnh bằng $120{}^\circ $. Diện tích toàn phần của hình nón là:
A. ${{\pi }^{2}}(3+\sqrt{3})$
B. $2\pi {{a}^{2}}(3+\sqrt{3})$
C. $2 \pi a^2$
D. $\pi a^2(3+2 \sqrt{3})$
Câu 6. Cho mặt cầu tâm $\mathrm{O}$, bán kính $\mathrm{R}=\mathrm{a}$. Một hình nón có đỉnh là $\mathrm{S}$ ở trên mặt cầu và đáy là đường tròn tương giao của mặt cầu đó với mặt phẳng vuông góc với đường thẳng $\mathrm{SO}$ tại $\mathrm{H}$ sao cho $\text{SH}=\frac{3a}{2}$. Độ dài đường sinh $l$ của hình nón bằng:
A. $I=a$
B. $I=a\sqrt{2}$
C. $I=a \sqrt{3}$
D. $I=2 a$
Câu 7. Cho hình nón đỉnh $S$ có đáy là hình tròn tâm $O$, bán kính $R$. Dựng hai đường sinh SA và SB, biết AB chắn trên đường tròn đáy một cung có số đo bằng $60{}^\circ $, khoảng cách từ tâm $\mathrm{O}$ đến mặt phẳng $(\mathrm{SAB})$ bằng $\frac{R}{2}$. Đường cao $\mathrm{h}$ của hình nón bằng:
A.$R\frac{\sqrt{6}}{4}$
B. $\frac{\text{R}\sqrt{3}}{2}$
C. $R \sqrt{3}$
D. $R \sqrt{2}$
Câu 8. Cho hình nón đỉnh $S$ có đáy là hình tròn tâm $O$. Dựng hai đường sinh SA và SB, biết tam giác $\mathrm{SAB}$ vuông và có diện tích bằng $4 \mathrm{a}^2$. Góc tạo bởi giữa trục $\mathrm{SO}$ và mặt phẳng $(\mathrm{SAB})$ bằng $30{}^\circ $. Đường cao $\mathrm{h}$ của hình nón bằng:
A. $\frac{a\sqrt{6}}{4}$
B. $\frac{\text{a}\sqrt{3}}{2}$
C. $a \sqrt{3}$
D. $a \sqrt{2}$
Câu 9. Cho hình nón đỉnh $\mathrm{S}$, đường cao $\mathrm{SO}$. Gọi $\mathrm{A}, \mathrm{B}$ là hai điểm thuộc đường tròn đáy của hình nón sao cho khoảng cách từ $O$ đến $\mathrm{AB}$ bằng a và \[\widehat{SAO}=30{}^\circ ,\,\,\widehat{SAB}=60{}^\circ \]. Độ dài đường sinh $l$ của hình nón bằng:
A. $a$
B. $a\sqrt{2}$
C. $a \sqrt{3}$
D. $2a$
Câu 10. Một hình nón có bán kính đáy $R$, góc ở đỉnh là $60{}^\circ $. Một thiết diện qua đỉnh nón chắn trên đáy một cung có số đo $90{}^\circ $. Diện tích của thiết diện là:
A. $\frac{{{R}^{2}}\sqrt{7}}{2}$
B. $\frac{{{R}^{2}}\sqrt{3}}{2}$
C. $\frac{3{{R}^{2}}}{2}$
D. $\frac{{{R}^{2}}\sqrt{6}}{2}$
Câu 11. Cho hình chóp tam giác đều $\mathrm{S} . \mathrm{ABC}$ có cạnh đáy bằng $2 \mathrm{a}$, khoảng cách từ tâm $\mathrm{O}$ của đường tròn ngoại tiếp của đáy $\mathrm{ABC}$ đến một mặt bên là $\frac{a}{2}$. Thể tích của khối nón đình $\mathrm{S}$ đáy là đường tròn ngoại tiếp tam giác $\mathrm{ABC}$ bằng:
A. $\frac{4 \pi a^3}{9}$
B. $\frac{4 \pi a^3}{3}$
C. $\frac{4 \pi a^3}{27}$
D. $\frac{4 \pi a^3}{3}$
Câu 12. Cho hình nón đỉnh $S$, đường cao $S O=h$, đường sinh $SA$. Nội tiếp hình nón là một hình chóp đỉnh $S$, đáy là hình vuông ABCD cạnh $a$. Nửa góc ở đỉnh của hình nón có tan bằng:
A. $\frac{h \sqrt{2}}{2 a}$
B. $\frac{a \sqrt{2}}{2 h}$
C. $\frac{a \sqrt{2}}{h}$
D. $\frac{h \sqrt{2}}{a}$
Câu 13. Cho hình trụ có hai đáy là hình tròn $(\mathrm{O})$ và $\left( \text{O }\!\!'\!\!\text{ } \right)$, chiều cao $R \sqrt{3}$, bán kính $\mathrm{R}$ và hình nón có đình là $\text{O}'$, đáy là hình tròn $(O ; R)$. Tính tỉ số giữa diện tích xung quanh của hình trụ và diện tích xung quanh của hình nón.
A. 2
B. $\sqrt{2}$
C. $\sqrt{3}$
D. 3
Câu 14. Một hình nón có chiều cao $9(\mathrm{~cm})$ nội tiếp trong một hình cầu có bán kính $5(\mathrm{~cm})$. Gọi $V_1, V_2$ lần lượt là thể tích của khối nón và khối cầu. Tính tỉ số $\frac{V_1}{V_2}$.
A. $\frac{81}{125}$.
B. $\frac{81}{500}$.
C. $\frac{27}{125}$.
D. $\frac{27}{500}$.
Câu 15. Cho hình nón có bán kính đáy là 5a, độ dài đường sinh là 13a. Thể tích khối cầu nội tiếp hình chóp bằng
A. $\frac{4000 \pi a^3}{81}$.
B. $\frac{4000 \pi a^3}{27}$.
C. $\frac{40 \pi a^3}{9}$.
D. $\frac{400 \pi a^3}{27}$.
ĐÁP ÁN
Câu 1. Hình minh họa
Đường sinh SA của hình nón hợp với đáy góc $\alpha =60{}^\circ \Rightarrow \widehat{SAO}=60{}^\circ $
$\begin{align}& \Rightarrow OA=SA\cdot \cos {{60}^{0}}=2a\cdot \frac{1}{2}=a \\ & \Rightarrow {{S}_{tp}}=\pi Rl+\pi {{R}^{2}}=\pi \cdot a\cdot 2a+\pi {{a}^{2}}=3\pi {{a}^{2}} \\ \end{align}$
Chọn B.
Câu 2. Hình minh họa
Đường kính đáy $\mathrm{d}=2 \mathrm{R}=2 \mathrm{a} \sqrt{2}$. Do góc ở đỉnh bằng $60{}^\circ $ nên thiết diện qua trục là tam giác đều.
Độ dài đường sinh là: $l=d=2a\sqrt{2}$
Diện tích xung quanh hình nón là:
${{S}_{xq}}=\pi Rl=\pi \cdot a\sqrt{2}\cdot 2a\sqrt{2}=4\pi {{a}^{2}}.$
Chọn A.
Câu 3.
Khi quay quanh tam giác $\mathrm{ABC}$ quanh trục $\mathrm{AB}$ ta được hình nón có độ dài đường sinh:
$l=BC=\sqrt{A{{B}^{2}}+A{{C}^{2}}}=\sqrt{{{a}^{2}}+3{{a}^{2}}}=2a$.
Chọn D.
Câu 4. Hình minh họa
Gọi S, O là đỉnh và tâm đường tròn đáy của hình nón, thiết diện qua đỉnh là tam giác SAB.
Theo giả thiết ta có tam giác SAB vuông cân tại $S$.
Đường sinh $l=SA=SB=a$.
Do đó bán kính
$r=O A=\frac{A B}{2}=\frac{\sqrt{S A^2+S B^2}}{2}=\frac{a \sqrt{2}}{2} .$
Diện tích xung quanh của hình nón:
$S_{x q}=\pi r l=\pi \cdot \frac{a \sqrt{2}}{2} \cdot a=\frac{\pi a^2 \sqrt{2}}{2} .$
Diện tích đáy $S=\pi r^2=\frac{\pi a^2}{2}$.
Vậy diện tích toàn phần của hình nón $(N)$ là:
$S_{t p}=S_{x q}+S_d=\frac{\pi a^2 \sqrt{2}}{2}+\frac{\pi a^2}{2}=\frac{\pi a^2(\sqrt{2}+1)}{2}$
Chọn A.
Câu 5. Gọi S, O là đỉnh và tâm đường tròn đáy của hình nón, thiết diện qua đỉnh là tam giác SAB.
Theo giả thiết, ta có $\mathrm{SA}=2 \mathrm{a}$ và $\widehat{ASO}=60{}^\circ $.
Trong tam giác SAO vuông tại $\mathrm{O}$, ta có
$OA=SA\cdot \sin 60{}^\circ =a\sqrt{3}.$
Vậy diện tích toàn phần:
${{S}_{tp}}=\pi R\ell +\pi {{R}^{2}}=\pi .OA\cdot SA+\pi {{(OA)}^{2}}=\pi {{a}^{2}}\left( 3+2\sqrt{3} \right)$
(dvdt).
Chọn B.
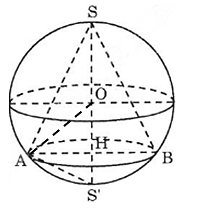
Câu 6. Hình vẽ minh họa
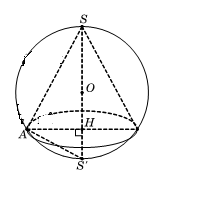
Gọi S’ là điểm đối xứng của S qua tâm O và A là một điểm trên đường tròn đáy của hình nón.
Tam giác SAS’ vuông tại A và có đường cao AH nên:
$S{{A}^{2}}=SH.SS'=2a.\frac{3a}{2}=3{{a}^{2}}\Rightarrow SA=a\sqrt{3}$
Chọn C.
Câu 7. Hình vẽ minh họa
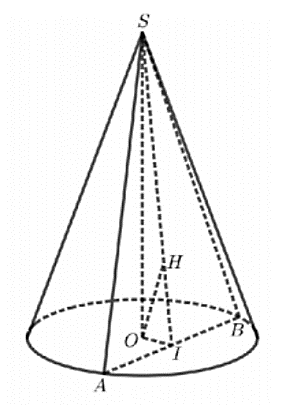
Gọi I là trung điểm của AB.
Kẻ OH vuông góc với SI.
$d_{(O,(S A B))}=O H=\frac{R}{2}$
Ta có cung $\widehat{A B}$ bằng $60{}^\circ $ nên $\widehat{AOB}=60{}^\circ $.
Tam giác AOI vuông tại I, ta có $\cos \widehat{I O A}=\frac{O I}{O A}$
$\Leftrightarrow OI=OA\cdot \cos 30{}^\circ =\frac{R\sqrt{3}}{2}$
Tam giác SOI vuông tại $\mathrm{O}$, ta có:
$\begin{align}& \frac{1}{O{{H}^{2}}}=\frac{1}{S{{O}^{2}}}+\frac{1}{O{{I}^{2}}} \\ & \Leftrightarrow \frac{1}{S{{O}^{2}}}=\frac{1}{O{{H}^{2}}}-\frac{1}{O{{I}^{2}}}=\frac{1}{{{\left( \frac{R}{2} \right)}^{2}}}-\frac{1}{{{\left( \frac{\sqrt{3}R}{2} \right)}^{2}}}=\frac{8}{3{{R}^{2}}} \\ & \Rightarrow SO=\frac{R\sqrt{6}}{4} \\ \end{align}$
Chọn A.
Câu 8. Hình vẽ minh họa
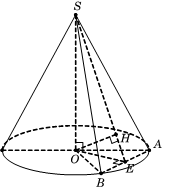
Theo giả thiết ta có tam giác SAB vuông cân tại S.
${{S}_{\text{SAB}}}=\frac{1}{2}SA.SB=4{{a}^{2}}\Rightarrow SA=SB=2a\sqrt{2}$
Gọi E là trung điểm AB, suy ra $SE=\frac{1}{2}AB$
$\left\{ \begin{array}{*{35}{l}}AB\bot OE \\AB\bot SO \\\end{array}\to AB\bot (SOE) \right.$.
Kẻ $OH\bot SE\to AB\bot OH\Rightarrow OH\bot (SAB)$
Ta có $S O \cap(S A B)=\{S\}$ và $OH\bot (SAB)\Rightarrow \widehat{(SO,(SAB))}=(\widehat{SO,SH})=\widehat{OSH}=30{}^\circ $
Ta có $AB=\sqrt{S{{A}^{2}}+S{{B}^{2}}}=4a\Rightarrow SE=\frac{1}{2}AB=2a\Rightarrow h=SE\cdot \cos 30{}^\circ =a\sqrt{3}$.
Chọn C.
Câu 9.
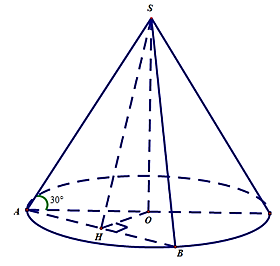
Gọi $H$ là trung điểm của AB, theo giả thiết ta có $O H=a$.
Tam giác SAB cân tại $S$ có góc $SAB=60{}^\circ $ nên là tam giác đều có cạnh
$S A=A B=2 A H=2 \sqrt{O A^2-O H^2}=2 \sqrt{R^2-a^2}$
với $R$ là bán kính của đáy hình nón.
Trong tam giác SAO có $SA=\frac{R}{\cos 30{}^\circ }=\frac{2R}{\sqrt{3}}$
Do đó
$2 \sqrt{R^2-a^2}=\frac{2 R}{\sqrt{3}} \Rightarrow R=\frac{a \sqrt{6}}{2}, l=S A=a \sqrt{2}$
Chọn B.
Câu 10. Hình minh họa
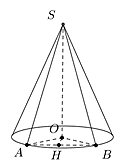
Thiêt diện là tam giác đều dẫn đến đường sinh là 2R.
Tam giác AOB vuông cân tại 0 nên $A B=R \sqrt{2} \Rightarrow H B=\frac{R}{\sqrt{2}} \Rightarrow S H=\sqrt{R^2-H B^2}=\frac{R \sqrt{14}}{2}$.
Khi đó ${{S}_{td}}=\frac{1}{2}SHAB=\frac{1}{2}\cdot \frac{R\sqrt{14}}{2}R\sqrt{2}=\frac{\sqrt{7}}{2}{{R}^{2}}$.
Chọn A.
Câu 11.
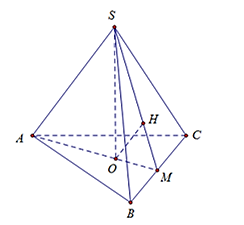
Ta có $O M=\frac{1}{3} A M=\frac{a \sqrt{3}}{3}$
Lại có $d(O ;(S B C))=O H=\frac{a}{2} \Rightarrow S O=a$
Mặt khác
$R_{(N)}=O A=\frac{2 a \sqrt{3}}{3} ; h=S O=a \Rightarrow V=\frac{1}{3} \pi R^2 h=\frac{4 \pi a^3}{9}$.
Chọn A.
Câu 12. Hình minh họa
Bán kính đáy là $R=\frac{a \sqrt{2}}{2} \Rightarrow \tan \frac{\alpha}{2}=\frac{R}{h}=\frac{a \sqrt{2}}{2 h}$.
Chọn B.
Câu 13. Hình minh họa
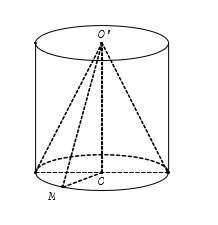
Diện tích xung quanh hình trụ là:
${{S}_{1}}=2\pi Rh=2\pi RR\sqrt{3}=2\pi {{R}^{2}}\sqrt{3}.$
Độ dài đường sinh của hình nón:
$l=\sqrt{R^2+h^2}=\sqrt{R^2+3 R^2}=2 R$
Diện tích xung quanh hình nón:
$S_2=\pi R l=\pi R .2 R=2 \pi R^2$
Vậy $\frac{S_1}{S_2}=\frac{2 \pi R^2 \sqrt{3}}{2 \pi R^2}=\sqrt{3}$
Chọn C.
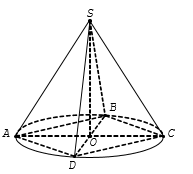
Câu 14.
Gọi hình cầu có tâm $\mathrm{O}$ bán kính R.Gọi hình nón có đình $S$, tâm đáy là $\mathrm{H}$, bán kính đáy $r=\mathrm{HA}$. Vì hình nón nội tiếp hình cầu nên đỉnh $\mathrm{S}$ thuộc hình cầu, chiều cao $\mathrm{SH}$ của hình nón đi qua tâm $\mathrm{O}$ của hình cầu, đồng thời cắt hình cầu tại điểm
$S^{\prime}$. Theo đề chiều cao hình nón $S H=9$, bán kính hình cầu $O S=5 \Rightarrow O H=4$, từ đó ta có $H A=\sqrt{O A^2-O H^2}=\sqrt{5^2-4^2}=3$
Thể tích khối nón
${{V}_{1}}=\frac{1}{3}h\pi {{r}^{2}}=\frac{1}{3}SH\cdot \pi \cdot H{{A}^{2}}=\frac{1}{3}\cdot 9.\pi {{.3}^{2}}=27\pi $
Thể tích khối cầu
${{V}_{2}}=\frac{4}{3}\pi {{R}^{3}}=\frac{4}{3}\pi {{5}^{3}}=\frac{500\pi }{3}\Rightarrow \text{ }\frac{{{V}_{1}}}{{{V}_{2}}}=\frac{27\pi }{\frac{500\pi }{3}}=\frac{81}{500}.$
Chọn B.
Câu 15. Hình minh họa
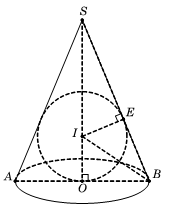
Hướng dẫn: Chiều cao của hình nón là $\sqrt{(13 a)^2-(5 a)^2}=12 a$. Gọi $r$ là bán kính nội tiếp mặt cầu
Ta có $\frac{r}{5 a}=\frac{12 a-r}{13 a} \Rightarrow r=\frac{10 a}{3} \Rightarrow V=\frac{4}{3} \pi r^3=\frac{4000 \pi a^3}{81}$.
Chọn A.
Các em đúng tất cả bao nhiêu câu trong 15 bài trên nhỉ? Hãy comment để Admin biết nhé!



















![Top 15 trường THPT tư thục tốt nhất TPHCM [Cập nhật mới 2023]](https://static.fqa.vn/fqa/sgk/top_truong_thpt_tu_thuc_tot_nhat_tphcm_be9958a086.jpg)





